library(Hotelling)
library(tidyverse)
library(here)
library(knitr)
library(purrr)
library(rmarkdown)
library(kableExtra)
library(flextable)1 확률벡터와 다변량 정규분포
다변량 자료(multivariate data)는 두 개 이상의 변수를 측정한 자료를 말합니다. 예를 들어, 학생들의 키와 몸무게, 시험 점수와 공부 시간, 나이와 소득 등이 다변량 자료에 해당합니다. 다변량 자료는 변수들 간의 관계를 분석하고 이해하는 데 중요한 역할을 합니다. 다변량 자료를 효과적으로 표현하고 분석하기 위해 다양한 그래프와 통계 기법이 사용됩니다. 이 장에서는 다변량 자료의 표현 방법과 분포를 이해하는 데 필요한 기본 개념과 도구들을 소개합니다.
1.1 예제- 국민체력100
국민체력100은 국민의 체력증진과 건강증진을 위해 개발된 종합적인 체력측정 프로그램이다. 이 프로그램은 다양한 연령대와 성별에 맞춘 체력측정 항목을 포함하고 있으며, 이를 통해 개인의 체력 상태를 평가하고 개선할 수 있는 기회를 제공한다.
이번 장에서는 청소년(13-18세) 남여 3000명에 대하여 2024년에 국민체력100 사업에서 측정한 자료를 예제로 사용하여 다변량 자료를 표현하는 방법들과 분포를 배울것이다.
먼저 측정항목에 대한 설명에 대한 자료를 보자.
load(here("data", "physical100.RData"))
ls()[1] "physical100_df" "physical100_df_info"먼저 데이터프레임 selected_var_df 에는 측정한 항목의 영문 변수이름(varname_eng), 종목의 설명(varname_kor), 측정분야(category_kor) 그리고 측정단위(unit) 가 다음과 같이 저장되어 있다.
varname_eng | varname_kor | category_kor | unit |
|---|---|---|---|
height | 신장 | 신체구성 | cm |
weight | 체중 | 신체구성 | kg |
body_fat_pct | 체지방율 | 신체구성 | |
grip_left | 악력_좌 | 근력 | kg |
grip_right | 악력_우 | 근력 | kg |
sit_forward | 앉아윗몸앞으로굽히기 | 유연성 | cm |
illinois | 일리노이 | 민첩성 | 초 |
hang_time | 청소년체공시간 | 순발력 | 초 |
twall_time | TWALL_시간 | 협응력 | 초 |
twall_errors | TWALL_실수 | 협응력 | 회 |
twall_score | TWALL_결과값 | 협응력 | 초 |
bmi | BMI | 신체구성 | |
rel_grip | 상대악력 | 근력 | % |
abs_grip | 절대악력 | 근력 | kg |
다음으로 청소년 3000명의 측정 자료의 일부는 다음과 같다.
sex | age | height | weight | body_fat_pct | grip_left | sit_forward |
|---|---|---|---|---|---|---|
남성 | 15 | 166.5 | 68.0 | 26.3 | 31.9 | 22.1 |
여성 | 13 | 166.4 | 45.5 | 22.0 | 20.0 | 10.2 |
남성 | 13 | 163.2 | 44.7 | 11.7 | 22.0 | -2.0 |
여성 | 14 | 156.9 | 44.7 | 26.9 | 17.3 | -5.0 |
남성 | 17 | 175.7 | 78.1 | 16.7 | 52.2 | 18.5 |
여성 | 16 | 167.2 | 74.5 | 37.1 | 25.9 | 12.0 |
여성 | 16 | 162.0 | 57.3 | 37.1 | 21.6 | -4.5 |
여성 | 17 | 169.1 | 75.0 | 39.8 | 21.6 | 0.1 |
여성 | 15 | 160.9 | 56.8 | 33.1 | 25.1 | -8.0 |
남성 | 13 | 162.8 | 57.6 | 18.0 | 39.6 | 28.0 |
1.2 확률벡터와 기본 성질
1.2.1 일변량 확률변수
일변량 확률변수(random variable) \(X\)가 확률밀도함수 \(f(x)\)를 가지는 분포를 따를때 기대값과 분산은 다음과 같이 정의된다.
\[ \begin{aligned} E(X) & = \int x f(x) dx = \mu\\ V(X) & = E[ X-E(X)]^2=\int (x-\mu)^2 f(x) dx =\sigma^2 \end{aligned} \]
새로운 확률변수 \(Y\)가 확률변수 \(X\)의 다음과 같은 선형변환으로 표시된다면 (\(a\)와 \(b\)는 실수)
\[ Y = aX+b \]
일변량 확률변수 \(X\)의 기대값(평균)과 분산은 다음과 같이 계산된다.
\[ \begin{aligned} E(Y) & = E(aX+b) \\ & = \int (ax+b) f(x) dx \\ & = a \int x f(x) dx + b \\ & = a E(X) + b\\ & = a \mu + b \end{aligned} \]
\[ \begin{aligned} V(Y) & = Var(aX+b) \\ & = E[aX+b -E(aX+b)]^2 \\ & = E[a(X-\mu)]^2 \\ & = a^2 E(X-\mu)^2\\ & = a^2 \sigma^2 \end{aligned} \]
1.2.2 다변량 확률벡터
이제 하나의 학률변수가 아는 2개 이상의 확률변수들을 모아놓은 확률벡터(random vector)를 생각해 보자. 다음과 같이 벡터로 표현된 확률벡터 \(\pmb X\)가 \(p\) 차원의 다변량 분포(multivariate distribution)를 따른다고 하고 결합확률밀도함수 \(f(\pmb x) =f(x_1,x_2,\dots,x_p)\)를 를 가진다고 하자.
\[ \pmb X = \begin{bmatrix} X_1 \\ X_2 \\ X_3 \\ .. \\ X_p \end{bmatrix} \]
다변량 확률벡터의 평균 벡터(mean vector)는 다음과 같이 주어진다. 확률벡터의 평균 벡터는 구성하는 각 확률변수의 평균으로 주어진다.
\[ \pmb E(\pmb X) = \begin{bmatrix} E(X_1) \\ E(X_2) \\ E(X_3) \\ .. \\ E(X_p) \end{bmatrix} = \begin{bmatrix} \mu_1 \\ \mu_2 \\ .. \\ \mu_p \end{bmatrix} =\pmb \mu \]
다음으로 공분산(covariance)과 상관계수(correlation coefficient)에 대해서 알아보자. 우리는 여러 개의 확률 변수의 관계를 분석하는 분석을 하려고 하는데, 이 경우 가장 많이 사용되는 통계량이 두 개의 변수들의 선형적 관계를 나타내는 상관계수이다. 두 확률변수 \(X_k\) 와 \(X_l\) 의 상관계수 \(\rho_{jk}\) 는 다음과 같이 정의된다.
\[ \rho_{jk} = \frac{Cov(X_j, X_k)}{ \sqrt{V(X_j) V(X_k)}} = \frac{\sigma_{jk}}{\sqrt{\sigma_{jj} \sigma_{kk}}}, \quad j,k=1,2,\dots,p \]
위의 상관계수의 공식에서 \(\sigma_{jj} \equiv \sigma^2_j\) 와 \(\sigma_{kk} = \sigma^2_k\) 는 각각 확률변수 \(X_i\) 와 \(X_j\) 의 분산이며, 공분산은 다음과 같이 정의된다.
\[ \begin{aligned} Cov(X_j, X_k) & = E [(X_j - E(X_j))(X_k - E(X_k))] \\ & = E(X_j X_k) - E(X_j)E(X_k) \end{aligned} \]
위의 식을 보면 각각의 확률 변수가 평균에서 차이가 나는 두 개의 편차, 즉 \(X_j - E(X_j)\), \(X_k - E(X_k)\) 의 곱에 대한 기대값으로 두 확률 변수가 평균에서 얼마나 같은 방향 또는 반대 방향으로 함께 움직이는 경향이 있는지 그 정도를 수치화한 값이다. 두 확률변수의 공분산의 값이 양의 값으로 커지면 두 확률 변수의 변화가 같은 방향으로 나타난다는 의미이며, 반대로 음의 값으로 커지면 두 확률 변수의 변화가 반대 방향으로 나타난다는 의미이다.
참고로 공분산은 단위가 확률 변수의 단위에 영향을 받기 떄문에 크기 자체만으로 비교가 직관적이지 않다는 단점이 있다. 반면에 상관 계수는 공분산을 각 확률 변수의 표분편차로 나누어 얻은 값이므로 단위에 영향을 받지 않아서 상대적인 비교가 가능하다.
상관계수는 -1 과 1 사이의 값을 가지며 1에 가까울수록 두 개의 변수가 같은 방향으로 움직이는 확률적 경향이 강해지며 반대로 -1 에 가까워질수록 반대의 방향을 움직이는 경향이 강해진다.
여기서 중요한 점은 상관계수(또는 공분산)은 두 확률 변수의 선형적 관계(linear relationship)을 나타내는 통계량으로 비선형적 관계를 파악하는데는 한계가 있을 수 있다.
이제 확률 벡터의 모든 변수에 대한 분산과 공분산을 다음과 같은 공분산 행렬로 나타낼 수 있다.
\[ \begin{aligned} V(\pmb X) & = Cov(\pmb X) = E (\pmb X-\pmb \mu) (\pmb X-\pmb \mu)^t \\ & = E(\pmb X \pmb X^t)-\pmb \mu \pmb \mu^t\\ & = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \dots & \sigma_{1p} \\ \sigma_{12} & \sigma_{22} & \dots & \sigma_{2p} \\ & \dots & \dots & \\ \sigma_{1p} & \sigma_{2p} & \dots & \sigma_{pp} \\ \end{bmatrix} \\ & = \pmb \Sigma \end{aligned} \]
여기서 \(\sigma_{jj}=V(X_j)\), \(\sigma_{jk} = Cov(X_j, X_k)=Cov(X_k, X_j)\) 이다. 따라서 공분산 행렬 \(\pmb \Sigma\)는 대칭행렬(symmetric matrix)이다.
더 나아가 확률 벡터의 모든 변수에 대한 상관계수을 다음과 같은 상관계수 행렬(correlation matrix) \(\pmb R\) 로 나타낼 수 있다.
\[ \begin{aligned} cor(\pmb X) & = \begin{bmatrix} 1 & \rho_{12} & \dots & \rho_{1p} \\ \rho_{12} & 1 & \dots & \rho_{2p} \\ & \dots & \dots & \\ \rho_{1p} & \rho_{2p} & \dots & 1 \\ \end{bmatrix} \\ & = \pmb R \end{aligned} \]
위의 상관계수 행렬에서 대각원소는 모두 1 임이 유의하자.
새로운 확률벡터 \(\pmb Y\)가 확률벡터 \(\pmb X\) 의 선형변환라고 하자.
\[ \pmb Y = \pmb A \pmb X + \pmb b \]
단 여기서 \(\pmb A\) 는 \(p \times p\) 실수 행렬이고 \(\pmb b\) 는 \(p \times 1\) 실수 벡터이다.
확률벡터 \(\pmb Y\)의 기대값(평균벡터)과 공분산은 다음과 같이 계산된다.
\[ \begin{aligned} E(\pmb Y ) &= E(\pmb A \pmb X+ \pmb b) \\ &= \pmb A E(\pmb X)+ \pmb b \\ &= \pmb A \pmb \mu+ \pmb b \\ V(\pmb Y) &= Var(\pmb A \pmb X+ \pmb b) \\ &= E[\pmb A \pmb X+ \pmb b -E(\pmb A \pmb X+ \pmb b)] [\pmb A \pmb X+ \pmb b -E(\pmb A \pmb X+ \pmb b)]^t \\ &= E[\pmb A \pmb X - \pmb A \pmb \mu] [\pmb A \pmb X - \pmb A \pmb \mu]^t \\ &= E[\pmb A (\pmb X - \pmb \mu)] [\pmb A (\pmb X - \pmb \mu)]^t \\ &= E [\pmb A(\pmb X - \pmb \mu) (\pmb X - \pmb \mu)^t \pmb A^t ] \\ &= \pmb A E [(\pmb X - \pmb \mu) (\pmb X - \pmb \mu)^t] \pmb A^t \\ &= \pmb A \pmb \Sigma \pmb A^t \end{aligned} \]
1.2.3 표본 통계량
이제 확률 표본(sample)을 이용하여 평균벡터, 공분산, 상관계수를 추정하는 간단한 방법에 대해서 알아보자.
확률 벡터 \(\pmb X\) 가 평균이 \(\pmb \mu\) 이고 공분산이 \(\pmb \Sigma\) 인 다변량 분포 \(F\) 를 따른다고 가정하자. 만약 확률 표본 \(\pmb X_1, \pmb X_2, \dots, \pmb X_n\) 이 독립적으로 다변량 분포 \(F\) 에서 임의로 추출되었다면
\[ \pmb X_i = \begin{bmatrix} X_{i1} \\ X_{i2} \\ X_{i3} \\ .. \\ X_{ip} \end{bmatrix} \quad i=1,2,\dots,n \]
다음과 같이 표본 통계량을 이용하여 평균벡터, 공분산, 상관계수를 추정할 수 있다.
먼저 다음과 같은 표본평균 벡터 \(\bar {\pmb X}\) 는 평균벡터 \(\pmb \mu\) 의 불편추정량(unbiased estimator)이다.
\[ \bar {\pmb X} = \begin{bmatrix} \bar X_1 \\ \bar X_2 \\ \bar X_3 \\ .. \\ \bar X_p \\ \end{bmatrix} = \begin{bmatrix} \sum_{i=1}^n X_{i1} / n \\ \sum_{i=1}^n X_{i2} / n \\ \sum_{i=1}^n X_{i3} / n \\ .. \\ \sum_{i=1}^n X_{ip} / n \end{bmatrix} = \hat {\pmb \mu} \]
여기서 \(X_{ij}\) 는 \(i\)번째 표본벡터 \(\pmb X_i =(X_{i1} X_{i2} \dots X_{ip})^t\)의 \(j\)번째 확률변수이다.
또한 아래에 주어진 표본 공분산 행렬 \(\pmb S\) 은 공분산 행렬 \(\pmb \Sigma\) 의 추정량이다.
\[ \pmb S = \begin{bmatrix} s_{11} & s_{12} & \dots & s_{1p} \\ s_{12} & s_{22} & \dots & s_{2p} \\ & \dots & \dots & \\ s_{1p} & s_{2p} & \dots & s_{pp} \\ \end{bmatrix} = \hat {\pmb \Sigma} \] 위에서 \(s_{jj} \equiv s^2_j\) 는 확률변수 \(X_j\) 의 표본 분산이며 \(s_{jk}\) 는 \(X_j\) 와 \(X_k\) 의 표본 공분산이며 다음과 같이 계산된다.
\[ s_{jj} = \frac{1}{n-1} \sum_{i=1}^n (X_{ij} - \bar X_j)^2, \quad s_{jk} = \frac{1}{n-1} \sum_{i=1}^n (X_{ij} - \bar X_j)(X_{ik} - \bar X_k), \quad j,k=1,2,\dots,p \]
마지막으로 아래에 주어진 표본 상관계수 행렬 \(\pmb R\) 은 상관계수 행렬 \(\pmb R\) 의 추정량이다.
\[ \hat {\pmb R} = \begin{bmatrix} 1 & r_{12} & \dots & r_{1p} \\ r_{12} & 1 & \dots & r_{2p} \\ & \dots & \dots & \\ r_{1p} & r_{2p} & \dots & 1 \\ \end{bmatrix} \]
여기서 \(r_{jk}\) 는 확률변수 \(X_j\) 와 \(X_k\) 의 표본 상관계수이며 다음과 같이 계산된다.
\[ r_{jk} = \frac{s_{jk}}{\sqrt{s_{jj} s_{kk}}}, \quad j,k=1,2,\dots,p \]
1.2.4 예제-국민체력100
이제 위에서 샇펴본 국민체력100 자료에서 청소년 남자 자료를 이용하여 평균벡터, 공분산 행렬, 상관계수 행렬의 표본 통계량을 계산해 보자.
먼저 표본 평균 벡터를 계산해 보자. 주어진 변수가 많으니 키(height), 몸무게(weight), 체지방률(body_fat_pct), 악력(grip_left), 앉아윗몸앞으로굽히기(sit_forward), 청소년체공시간(hang_time) 6개 변수만 선택하여 계산해 보자.
# 국민체력100 자료에서 남자만 선택하여 데이터프레임 df 생성
df <- physical100_df %>%
filter(sex == "남성") %>%
select(height, weight, body_fat_pct, grip_left, sit_forward,hang_time)
# 패키지 dplyr의 summarise()와 across() 함수를 사용하여 각 열의 평균 계산
sample_mean_vector <- df %>%
summarise(across(everything(), \(x) mean(x, na.rm = TRUE))) %>%
unlist()
sample_mean_vector height weight body_fat_pct grip_left sit_forward hang_time
172.0451492 69.7115470 20.9993923 36.0728729 7.8976630 0.5593964 다음으로 표본 공분산 행렬을 계산해 보자.
cor(df) height weight body_fat_pct grip_left sit_forward
height 1.0000000000 0.50994161 -0.03019400 0.45225668 0.0008938941
weight 0.5099416134 1.00000000 0.69156075 0.46152254 0.0111910927
body_fat_pct -0.0301940037 0.69156075 1.00000000 -0.01208826 -0.1434596849
grip_left 0.4522566754 0.46152254 -0.01208826 1.00000000 0.2605654264
sit_forward 0.0008938941 0.01119109 -0.14345968 0.26056543 1.0000000000
hang_time 0.1884978140 -0.14265212 -0.48446817 0.34559521 0.2889235491
hang_time
height 0.1884978
weight -0.1426521
body_fat_pct -0.4844682
grip_left 0.3455952
sit_forward 0.2889235
hang_time 1.0000000마지막으로 표본 상관계수 행렬을 계산해 보자.
cor(df) height weight body_fat_pct grip_left sit_forward
height 1.0000000000 0.50994161 -0.03019400 0.45225668 0.0008938941
weight 0.5099416134 1.00000000 0.69156075 0.46152254 0.0111910927
body_fat_pct -0.0301940037 0.69156075 1.00000000 -0.01208826 -0.1434596849
grip_left 0.4522566754 0.46152254 -0.01208826 1.00000000 0.2605654264
sit_forward 0.0008938941 0.01119109 -0.14345968 0.26056543 1.0000000000
hang_time 0.1884978140 -0.14265212 -0.48446817 0.34559521 0.2889235491
hang_time
height 0.1884978
weight -0.1426521
body_fat_pct -0.4844682
grip_left 0.3455952
sit_forward 0.2889235
hang_time 1.0000000표본 상관계수 행렬을 보면 다양한 상관관계가 나타나는데 이러한 관계를 더 자세하게 보기위하여 산점도 행렬(scatterplot matrix)로 시각화 하면 더 유용한 정보를 얻을 수 있다.
pairs(df, pch=19, col='blue', cex=0.1)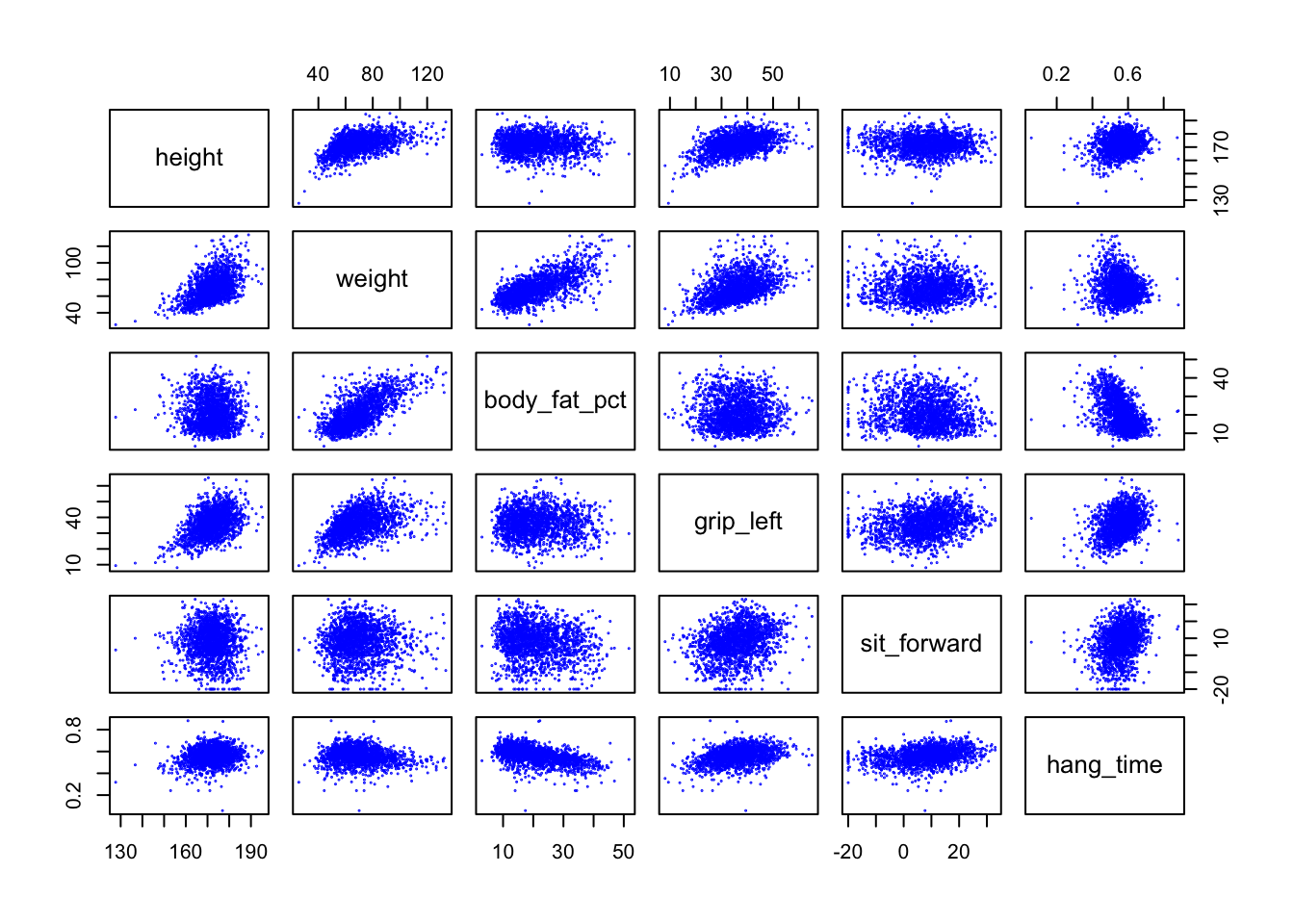
1.3 다변량 정규분포
일변량 확률변수 \(X\)가 평균이 \(\mu\) 이고 분산이 \(\sigma^2\)인 정규분포를 따른다면 다음과 같이 나타내고 \[ X \sim N(\mu, \sigma^2 ) \] 확률밀도함수 \(f(x)\) 는 다음과 같이 주어진다.
\[ f(x) = (2 \pi \sigma^2)^{-1/2} \exp \left ( - \frac{(x-\mu)^2}{2} \right ) \]
1.3.1 확률 밀도 함수
\(p\)-차원 확률벡터 \(\pmb X\)가 평균이 \(\pmb \mu\) 이고 공분산이 \(\pmb \Sigma\)인 다변량 정규분포를 따른다면 다음과 같이 나타내고 \[ \pmb X \sim N_p(\pmb \mu, \pmb \Sigma ) \] 확률밀도함수 \(f(\pmb x)\) 는 다음과 갇이 주어진다.
\[ f(\pmb x) = (2 \pi)^{-p/2} | \pmb \Sigma|^{-1/2} \exp \left ( - \frac{(\pmb x-\pmb \mu) \pmb \Sigma^{-1}(\pmb x-\pmb \mu)^t}{2} \right ) \]
예를 들어 \(2\)-차원 확률벡터 \(\pmb X=(X_1, X_2)^t\)가 평균이 \(\pmb \mu=(\mu_1,\mu_2)^t\) 이고 공분산 \(\pmb \Sigma\)가 다음과 같이 주어진
\[ \pmb \Sigma = \begin{bmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{12} & \sigma_{22} \end{bmatrix} \]
이변량 정규분포를 따른다면 확률밀도함수 \(f(\pmb x)\)에서 \(\exp\)함수의 인자는 다음과 같이 주어진다. \[ \begin{aligned} &(\pmb x-\pmb \mu) \pmb \Sigma^{-1}(\pmb x-\pmb \mu)^t = \\ &-\frac{1}{2 (1-\rho^2)} \left [ \left ( \frac{(x_1-\mu_1)^2}{\sigma_{11}} \right ) +\left ( \frac{(x_2-\mu_2)^2}{\sigma_{22}} \right ) -2 \rho \left ( \frac{(x_1-\mu_1)}{\sqrt{\sigma_{11}}} \right ) \left ( \frac{(x_2-\mu_2)}{\sqrt{\sigma_{22}}} \right ) \right ] \end{aligned} \]
그리고 \(p=2\) 인 경우 확률밀도함수의 상수부분은 다음과 같이 주어진다.
\[ (2 \pi)^{-p/2} | \pmb \Sigma|^{-1/2} = \frac{1}{ 2 \pi \sqrt{\sigma_{11} \sigma_{22} (1-\rho^2)}} \]
여기서 \(\rho = \sigma_{12} / \sqrt{\sigma_{11} \sigma_{22}}\)
다변량 정규분포에서 공분산이 0인 두 확률 변수는 독립이다. \[ \sigma_{ij} = 0 \leftrightarrow X_i \text{ and } X_j \text{ are independent} \]
참고로 정규분포가 아닌 다른 분포의 경우 공분산이 0인 두 확률 변수는 독립이 아닐 수 있다.
1.3.2 예제-국민체력100
이제 위에서 샇펴본 국민체력100 자료에서 청소년 남자의 키(height)와 몸무게(weight) 가 이변량 정규분포를 따른다고 가정하고 확률밀도 함수를 그려보자.
# 필요한 패키지 로드
library(mvtnorm)
library(plotly)
# 국민체력100 자료에서 남자만 선택하여 데이터프레임 df 생성, 키와 몸무게 변수만 선택와
df <- physical100_df %>%
filter(sex == "남성") %>%
select(height, weight)
# 패키지 dplyr의 summarise()와 across() 함수를 사용하여 각 열의 평균 계산
sample_mean_vector <- df %>%
summarise(across(everything(), \(x) mean(x, na.rm = TRUE))) %>%
unlist()
sample_mean_vector height weight
172.04515 69.71155 # 표본 공분산 행렬 계산
sample_cov_matrix <- cov(df, use = "complete.obs")
sample_cov_matrix height weight
height 47.51166 54.80339
weight 54.80339 243.09372# 이변량 정규분포의 확률밀도함수 계산
# 키와 몸무게의 평균에서 표분편차 3배의 범위의 값을 100개로 나누어 x,y 축 생성
x1_seq <- seq(sample_mean_vector[1]-3* sqrt(sample_cov_matrix[1,1]), sample_mean_vector[1]+3* sqrt(sample_cov_matrix[1,1]), length.out = 100)
x2_seq <- seq(sample_mean_vector[2]-3* sqrt(sample_cov_matrix[2,2]), sample_mean_vector[2]+3* sqrt(sample_cov_matrix[2,2]), length.out = 100)
grid <- expand.grid(height = x1_seq, weight = x2_seq)
# 확률밀도함수 계산 (z축의 값)
grid$z <- dmvnorm(grid, mean = sample_mean_vector, sigma = sample_cov_matrix)
# z를 행렬로 변환 (surface plot용)
z_matrix <- matrix(grid$z, nrow = length(x1_seq), ncol = length(x2_seq))다음은 위에서 얻어진 확률밀도 함수를 3차원 surface plot으로 나타낸 것이다.
# 이변량 정규분포의 확률밀도 함를 3D Surface Plot
plot_ly(
x = x1_seq,
y = x2_seq,
z = z_matrix
) %>% add_surface() %>%
layout(
title = "Bivariate Normal PDF (Surface)",
scene = list(
xaxis = list(title = "키"),
yaxis = list(title = "몸무게"),
zaxis = list(title = "Density")
)
)아래 그림은 표본으로 부터 얻어진 확률밀도 함수를 2차원 등고선(contour)으로 나타낸 그림이다.
plot_ly(
x = x1_seq,
y = x2_seq,
z = z_matrix
) %>%
add_contour(
contours = list(
coloring = "heatmap",
showlabels = TRUE
)
) %>%
layout(
title = "Bivariate Normal PDF (Contour)",
xaxis = list(title = "키"),
yaxis = list(title = "몸무게")
)1.3.3 조건부 분포
다변량 정규분포 \(N(\pmb \mu, \pmb \Sigma)\)를 따르는 확률벡터 \(\pmb X\)를 다음과 같이 두 부분으로 나누면
\[ \pmb X = \begin{bmatrix} \pmb X_1 \\ \pmb X_2 \end{bmatrix}, \quad \pmb X_1 = \begin{bmatrix} \pmb X_{11} \\ \pmb X_{12} \\ \pmb \vdots \\ \pmb X_{1p} \end{bmatrix}, \quad \pmb X_2= \begin{bmatrix} \pmb X_{21} \\ \pmb X_{22} \\ \pmb \vdots \\ \pmb X_{2q} \end{bmatrix} \]
각각 다변량 정규분포를 따르고 다음과 같이 나타낼 수 있다.
\[ \begin{bmatrix} E(\pmb X_1) \\ E(\pmb X_2) \end{bmatrix} = \begin{bmatrix} \pmb \mu_1 \\ \pmb \mu_2 \end{bmatrix} , \quad \begin{bmatrix} V(\pmb X_1) & Cov(\pmb X_1, X_2) \\ Cov(\pmb X_2 X_1) & V(\pmb X_2) \end{bmatrix} = \begin{bmatrix} \pmb \Sigma_{11} & \pmb \Sigma_{12} \\ \pmb \Sigma^t_{12} & \pmb \Sigma_{22} \end{bmatrix} \]
\[ \pmb X = \begin{bmatrix} \pmb X_1 \\ \pmb X_2 \end{bmatrix} \sim N_{p+q} \left ( \begin{bmatrix} \pmb \mu_1 \\ \pmb \mu_2 \end{bmatrix} ,\begin{bmatrix} \pmb \Sigma_{11} & \Sigma_{12} \\ \pmb \Sigma^t_{12} & \Sigma_{22} \end{bmatrix} \right ) \]
확률벡터 \(\pmb X_2 = \pmb x_2\)가 주어진 경우 \(\pmb X_1\)의 조건부 분포는 \(p\)-차원 다변량 정규분포를 따르고 평균과 공분산은 다음과 같다.
\[ E(\pmb X_1 | \pmb X_2 = \pmb x_2 ) = \pmb \mu_1 + \pmb \Sigma_{12} \pmb \Sigma^{-1}_{22} (\pmb \mu_2 - \pmb x_2), \quad V(\pmb X_1 | \pmb X_2 = \pmb x_2 ) = \pmb \Sigma_{11} -\pmb \Sigma_{12} \pmb \Sigma^{-1}_{22} \pmb \Sigma^t_{12} \]
만약 \(X_2 = x_2\)가 주어졌을 때 \(X_1\)의 조건부 분포는 정규분포이고 평균과 분산은 다음과 같이 주어진다.
\[ E( X_1 | X_2 = x_2 ) = \mu_1 + \frac{\sigma_{12}}{\sigma_{22}} ( \mu_2 - x_2) = \mu_1 + \rho \frac{\sqrt{\sigma_{11}}}{\sqrt{\sigma_{22}}} ( \mu_2 - x_2) \]
\[ V( X_1 | X_2 = x_2 ) = \sigma_{11} - \frac{\sigma^2_{12}}{\sigma_{22}} = \sigma_{11}(1-\rho^2) \]