블럭설계 예제
다음은 교과서 예제 5.1 -플라스틱 강도 실험을 분석하는 예제이다.
플라스틱 제품의 강도를 측정하는 것이 실험의 목적이다. 랜덤하게 4일을 택해서 각 일마다 온도를 3개 수준으로 랜덤하게 변화시켜서 제품의 강도(intensity)를 측정하였다.
여기서 온도(temp)는 고정효과(\(\tau\) )이며 선택된 일(day)는 블럭(\(\rho\) )에 따른 효과이다.
\[ x_{ij} = \mu + \tau_i + \rho_j + e_{ij} \]
자료의 구성
이제 실험자료를 입력하여 데이터프레임으로 만들어 보자
<- c (98.0 , 97.7 , 96.5 ,99.0 , 98.0 , 97.9 ,98.6 , 98.2 , 96.9 ,97.6 , 97.3 , 96.7 )<- factor (rep (c (70 , 80 , 90 ), times= 4 ))<- as.factor (rep (c (1 : 4 ), each= 3 ))<- data.frame (intensity= intensity, temp= temp, day= day)
intensity temp day
1 98.0 70 1
2 97.7 80 1
3 96.5 90 1
4 99.0 70 2
5 98.0 80 2
6 97.9 90 2
7 98.6 70 3
8 98.2 80 3
9 96.9 90 3
10 97.6 70 4
11 97.3 80 4
12 96.7 90 4
벡터를 범주형 변수로 만들어 줄때 두 함수 as.factor() 와 factor() 모두 사용 가능하다.
시각적 분석
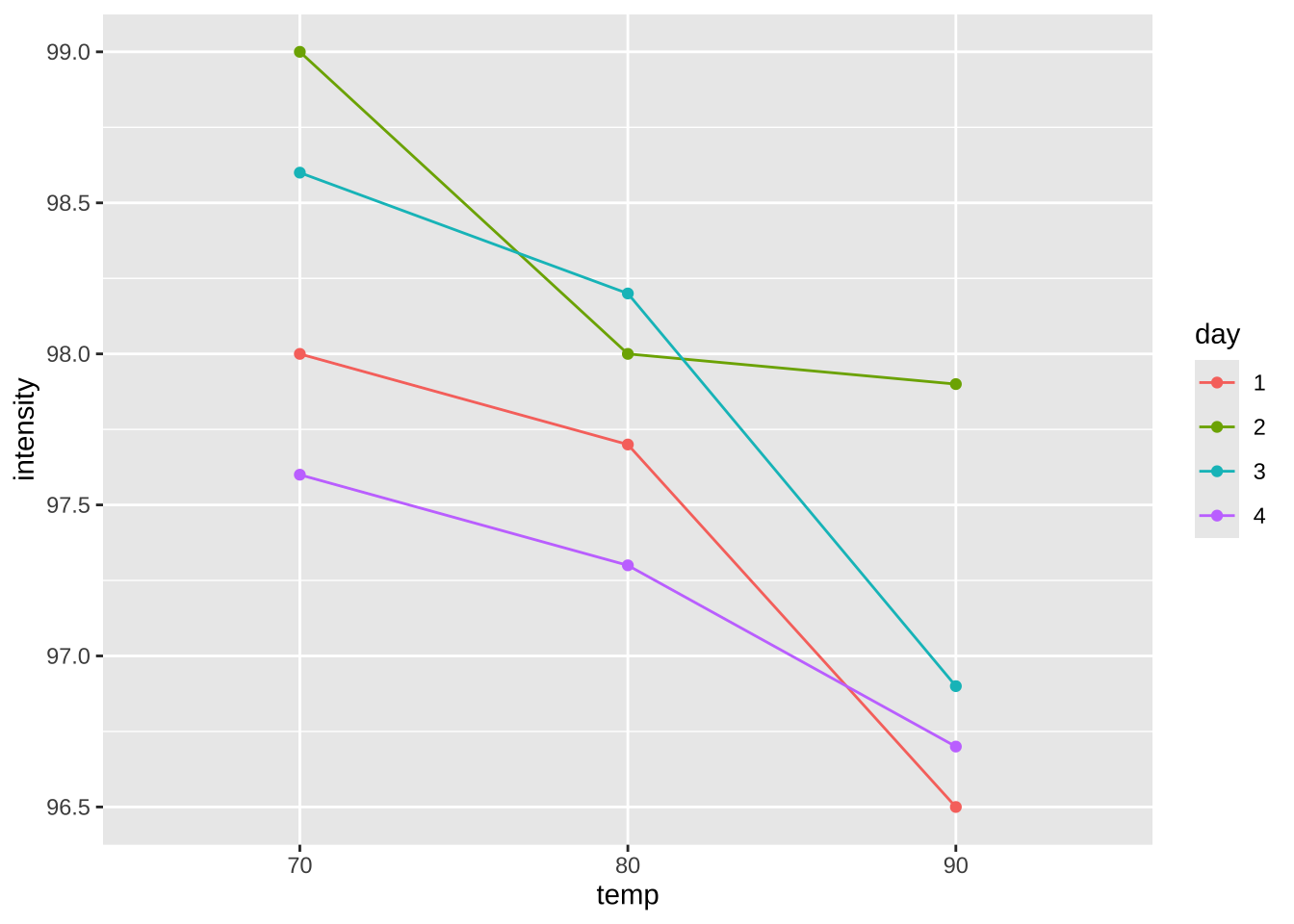
이제 온도의 수준에 따른 변화를 볼 수 있는 그림을 그려보자. 온도가 올라가면 강도가 떨어지는 경향을 볼 수 있다.
%>% ggplot (aes (x = temp , y = intensity, color= day)) + geom_line (aes (group = day)) + geom_point ()
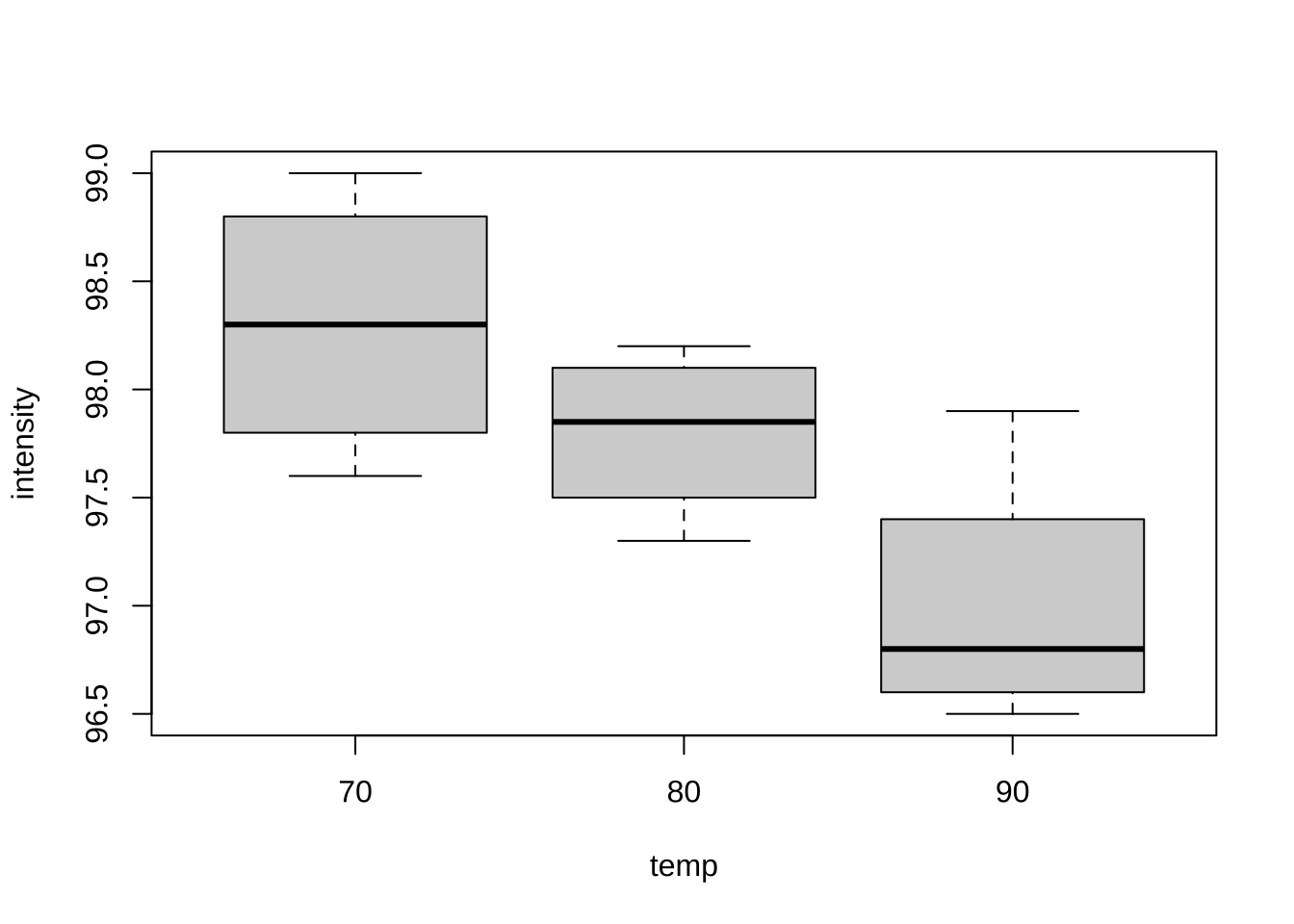
plot (intensity ~ temp, data= df)
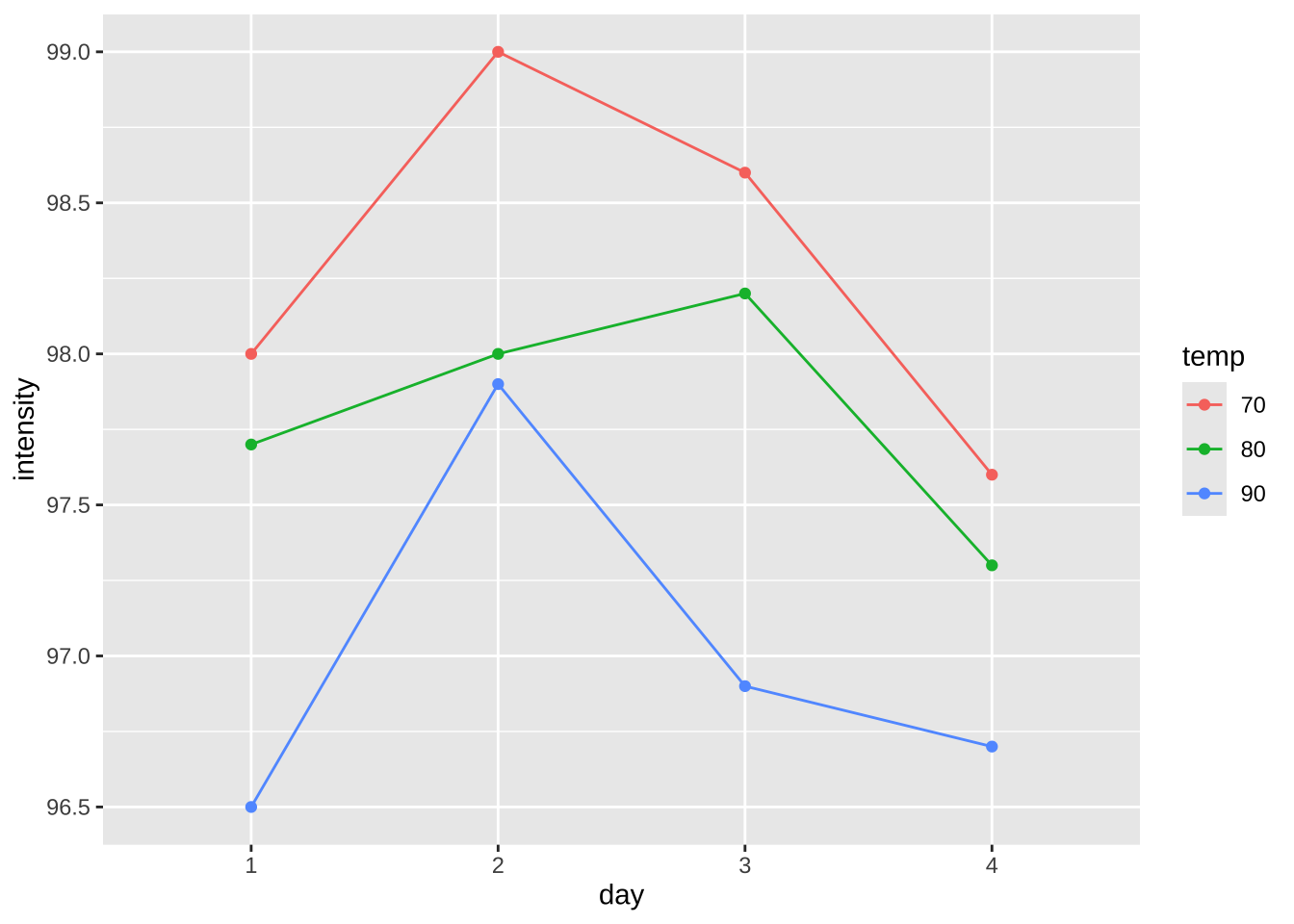
이제 실험일에 따른 변동을 살펴보자. 실험일에 따라서 온도의 효과가 변하는 것을 볼 수 있다. 단 실험일과 온도의 상호작용은 크게 나타나지 않는다. 유의할 점은 반복이 없기 때문에 상호작용에 대한 추론은 불가능하다
%>% ggplot (aes (x = day , y = intensity, color= temp)) + geom_line (aes (group = temp)) + geom_point ()
분산분석
블럭 효과인 실험일(day)를 고정효과 로 놓았을 경우 분산분석표는 다음과 같다.
\[ \rho_j : \text{ fixed effect,} \quad e_{ij} \sim N(0, \sigma_E^2) \]
<- aov (intensity ~ temp + day, data= df)summary (model)
Df Sum Sq Mean Sq F value Pr(>F)
temp 2 3.44 1.7200 18.429 0.00274 **
day 3 2.22 0.7400 7.929 0.01647 *
Residuals 6 0.56 0.0933
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
위의 분산분석표에서 온도의 효과를 검정하는 F-통계량의 값은 18.4285714 이고 p-값은 0.002744이다. 따라서 5% 유의수준으로 귀무가설을 기각하며 온도에 따라서 강도는 유의하게 다르다.
일반적으로 블럭효과에 대해서는 검정하지 않지만 그래도 p-값이 0.0164702 로서 매우 작으므로 실험일에 따른 변동이 크다는 것을 알 수 있다. 이는 실험울 수행하는 날에 따라서 관측값에 변동이 크다는 것이다. 단 상호작용이 그림으로 볼 때 나타나지 않기 때문에 온도의 효과는 적절하게 추정할 수 있다.
혼합모형
고정효과와 임의효과(변량)가 동시에 모형식에 나타나는 모형을 혼합모형(mixed models)이라고 부른다. 교과서에서는 변량모형이라고 부른다. 혼합모형에 대한 자세한 기초이론은 부록 C
혼합모형을 적합시키는 패키지는 lme4 이며 모형을 적합시키는 함수는 lmer이다.
library(lme4)
library(lmerTest)
혼합모형으로 부터 얻은 분산분석표에서 p-값을 보려면 패키지 lmerTest를 사용해야 한다.
함수 lmer 에서 고정효과에 대한 모형식은 함수 anova와 같다.
함수 lmer 에서 만약 변수 var 을 임의효과로 고려하려면 (1|var) 으로 쓰면 된다.
다음은 플라스틱 강도 자료 실험에서 블럭 효과인 실험일(day, \(\rho\) )를 임의효과 로 놓았을 경우 분석결과이다. 즉
\[ \rho_j \sim N(0, \sigma_B^2), \quad e_{ij} \sim N(0, \sigma_E^2) \]
<- lmer (intensity ~ temp + (1 | day), data= df)summary (fit)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: intensity ~ temp + (1 | day)
Data: df
REML criterion at convergence: 14.6
Scaled residuals:
Min 1Q Median 3Q Max
-1.0616 -0.7992 0.1430 0.5419 1.2297
Random effects:
Groups Name Variance Std.Dev.
day (Intercept) 0.21556 0.4643
Residual 0.09333 0.3055
Number of obs: 12, groups: day, 4
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 98.3000 0.2779 4.5593 353.739 2.7e-11 ***
temp80 -0.5000 0.2160 6.0000 -2.315 0.05989 .
temp90 -1.3000 0.2160 6.0000 -6.018 0.00095 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) temp80
temp80 -0.389
temp90 -0.389 0.500
위의 결과에서 블럭효과(day) 를 나타내는 분산 성분 \(\sigma_B^2\) 의 추정치는 0.2155556 이며 오차항(Residual)의 분산 \(\sigma_E^2\) 의 추정치는 0.0933333 이다. 이는 급내상관 계수(ICC)는 0.6978417 로서 매우 크다는 것을 의미한다.
\[ ICC = \frac{\sigma_B^2}{\sigma_B^2 + \sigma_E^2} = 0.6978417 \]
다음은 플라스틱 강도 자료 실험에서 블럭 효과를 임의효과로 놓았을 경우 분산분석표이다. 함수 lmer 에 의해 생성된 결과를 함수 anova에 적용하면 고정효과에 대한 분산분석과 F-검정만 보여준다. 앞에서 블럭을 고정효과로 놓았을 때 분산분석의 검정 결과와 같다.
Type III Analysis of Variance Table with Satterthwaite's method
Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
temp 3.44 1.72 2 6 18.429 0.002744 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
라틴정방설계
로켓 추진체
다음은 교재 예제 5.2 - 로켓 추진체 실험을 분석하는 예제이다.
5가지의 로켓 추진체(A, B, C, D, E)의 성능을 비교하기 위하여 라틴정방계획을 사용한 실험이다.
행블럭: 5개의 연료 (R, \(\rho\) )
열블럭: 5명의 기사 (C, \(\gamma\) )
처리: 5가지의 로켓 추진체 (trt, \(\tau\) )
[ x_{ijk} = + _i + _j + k + e {ijk } ]
자료의 구성
예제 5.2에 있는 자료를 분석을 위하여 데이터프레임으로 만들어 보자.
<- c ("A" , "B" , "C" , "D" , "E" ,"B" , "C" , "D" , "E" , "A" ,"C" , "D" , "E" , "A" , "B" ,"D" , "E" , "A" , "B" , "C" ,"E" , "A" , "B" , "C" , "D" )<- factor (trt)<- factor (rep (1 : 5 , each= 5 ))<- factor (rep (1 : 5 , times= 5 ))<- c ( - 1 ,- 5 , - 6 , - 1 , - 1 ,- 8 , - 1 , 5 , 2 , 11 ,- 7 , 13 , 1 , 2 , - 4 ,1 , 6 , 1 , - 2 , - 3 ,- 3 , 5 , - 5 , 4 , 6 )<- data.frame (trt, R, C, y)
trt R C y
1 A 1 1 -1
2 B 1 2 -5
3 C 1 3 -6
4 D 1 4 -1
5 E 1 5 -1
6 B 2 1 -8
7 C 2 2 -1
8 D 2 3 5
9 E 2 4 2
10 A 2 5 11
11 C 3 1 -7
12 D 3 2 13
13 E 3 3 1
14 A 3 4 2
15 B 3 5 -4
16 D 4 1 1
17 E 4 2 6
18 A 4 3 1
19 B 4 4 -2
20 C 4 5 -3
21 E 5 1 -3
22 A 5 2 5
23 B 5 3 -5
24 C 5 4 4
25 D 5 5 6
함수 xtabs()는 모형식을 이용하여 다음과 같이 열과 행으로 구성된 자료를 보여줄 수 있다.
xtabs (y~ R + C, data = df)
C
R 1 2 3 4 5
1 -1 -5 -6 -1 -1
2 -8 -1 5 2 11
3 -7 13 1 2 -4
4 1 6 1 -2 -3
5 -3 5 -5 4 6
시각적 분석
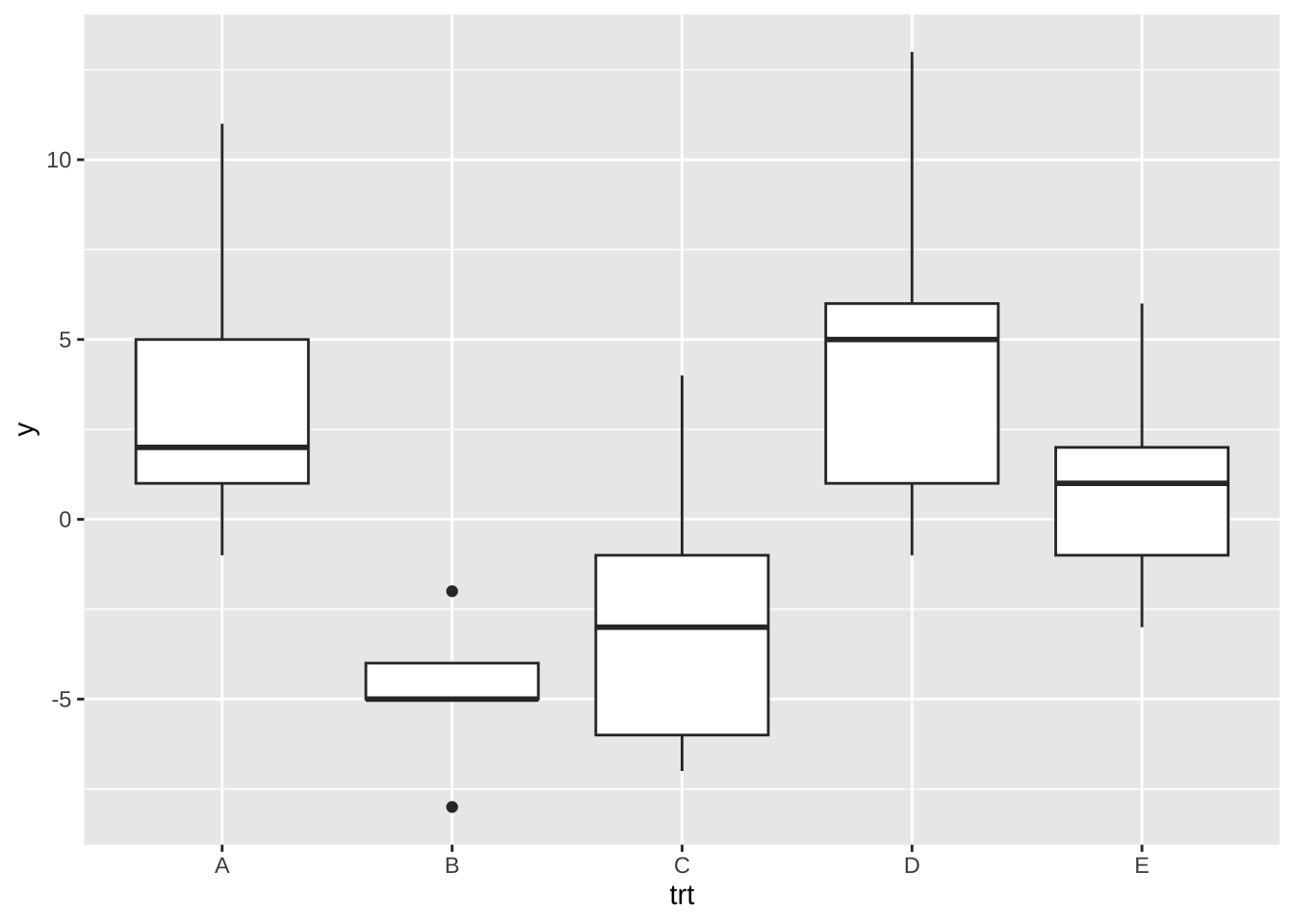
먼저 로켓 추진체, 즉 처리별로 자료의 분포를 보자. 추진체 B 와 C 가 다른 추진체들 보다 관측값이 작게 나오는 것을 알 수 있다.
%>% ggplot () + aes (x = trt , y = y) + geom_boxplot ()
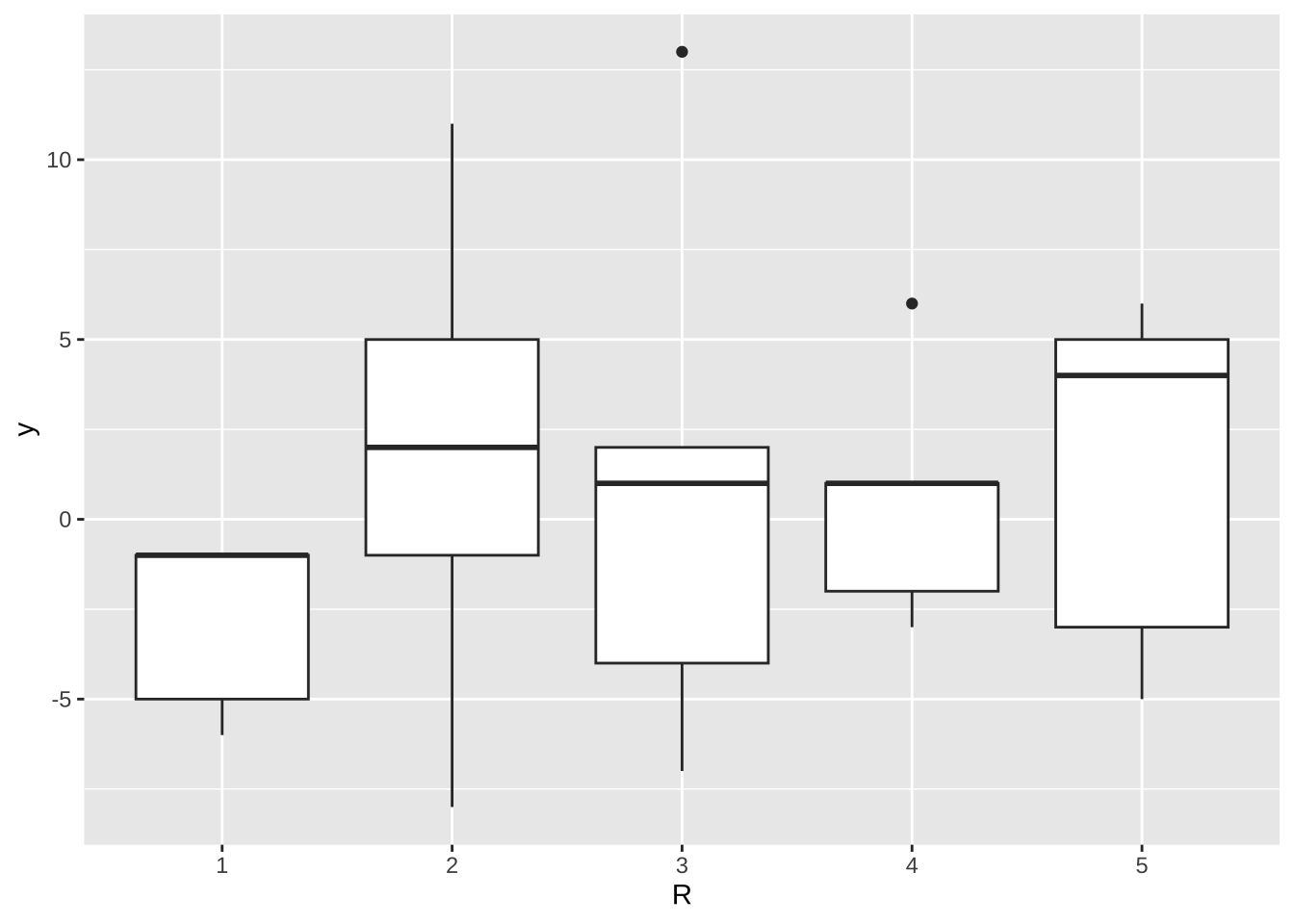
원료(R) 뭉치별로 자료의 분포를 보면 큰 차이는 보이지 않는다.
%>% ggplot () + aes (x = R , y = y) + geom_boxplot ()
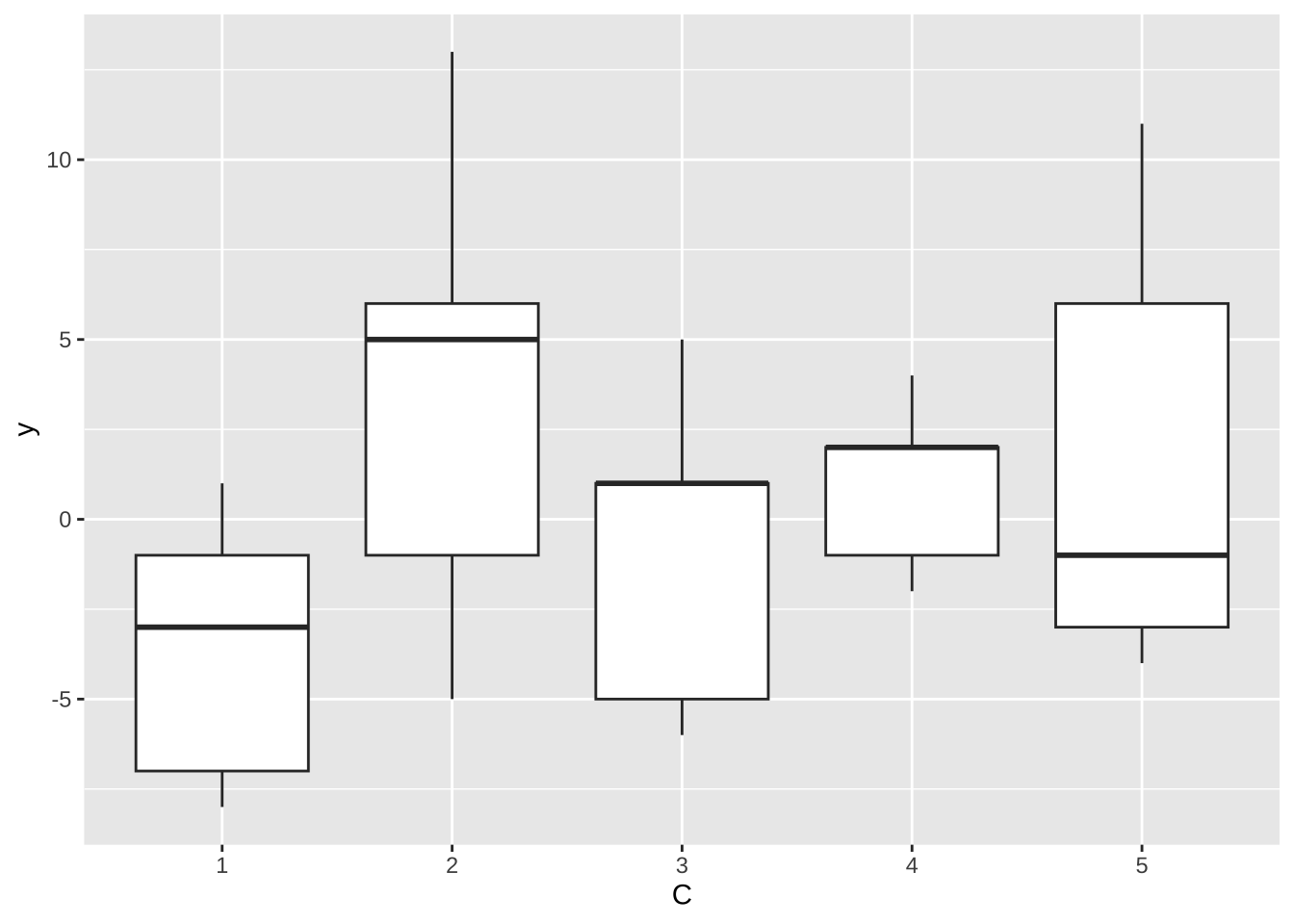
기사(C) 별로 자료의 분포를 보면 약간의 차이가 보인다.
%>% ggplot () + aes (x = C , y = y) + geom_boxplot ()
분산분석
이제 라틴정방계획법으로 얻은 자료에 대래 분산분석을 적용해 보자.
<- aov (y ~ trt + R + C, data= df)summary (model)
Df Sum Sq Mean Sq F value Pr(>F)
trt 4 330 82.50 7.734 0.00254 **
R 4 68 17.00 1.594 0.23906
C 4 150 37.50 3.516 0.04037 *
Residuals 12 128 10.67
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
위의 분산분석표에서 추진체(처리)의 효과를 검정하는 F-통계량의 값은 7.734375 이고 p-값은 0.0025365이다. 따라서 5% 유의수준으로 귀무가설을 기각하며 추진체에 따라서 성능이 유의하게 다르다.
라틴정방의 구축
교과서 5.3절에서는 라틴정방 계획으로 실험을 하는 경우 처리를 랜덤하게 배정하는 방법을 설명하고 있다.
패키지 agricolae 에 포함된 함수 design.lsd()를 이용하면 다음과 같이 처리를 랜덤하게 배정해준다.
<- factor (c ("A" , "B" , "C" , "D" , "E" ))
[1] A B C D E
Levels: A B C D E
[,1] [,2] [,3] [,4] [,5]
[1,] "D" "E" "C" "A" "B"
[2,] "B" "C" "A" "D" "E"
[3,] "A" "B" "E" "C" "D"
[4,] "E" "A" "D" "B" "C"
[5,] "C" "D" "B" "E" "A"
함수 design.lsd()는 실행할 때마다 랜덤하게 배정하기 때문에 기록을 위해서 랜덤 seed 를 지정하면 나중에도 동일한 계획을 얻을 수 있다.
design.lsd (mytrt, seed = 1234 )$ sketch
[,1] [,2] [,3] [,4] [,5]
[1,] "C" "B" "E" "A" "D"
[2,] "A" "E" "C" "D" "B"
[3,] "B" "A" "D" "E" "C"
[4,] "D" "C" "A" "B" "E"
[5,] "E" "D" "B" "C" "A"
처리 조합의 블럭
화학약품의 생성률
다음은 교재 분할법 I - 예제 5.3 - 화학약품의 생성률 실험을 분석하는 예제이다.
이 실험에서는 화학약품의 생성률에 영향을 미치는 두 요인을 고려한 실험이다.
반응온도(temp, \(\alpha\) ) 3개의 수준
중간원료 제조회사 (company, \(\beta\) ) 3개의 수준
이 실험에서는 9개의 처리를 먼저 랜덤하게 선택하고 선택된 처리 하에서 실험을 2번 반복하였다. 따라서 처리의 조합이 블럭효과(block, \(\rho\) )로 나타난다.
\[ x_{ijk} = \mu + \alpha_i + \beta_j + \rho_{ij} + e_{2(ijk)} \]
위의 모형식에서 상호작용 효과 \((\alpha \beta)_{ij}\) 와 1차 랜덤화에 의한 오차 \(e_{1(ij)}\) 는 교락되어 블럭효과 \(\rho_{ij}\) 에 합쳐저서 나타난다.
\[ \rho_{ij} = e_{1(ij)} + (\alpha \beta)_{ij} \]
이러한 경우 블럭효과 \(\rho_{ij}\) 는 임의효과가 된다.
\[
\rho_{ij} \sim N(0, \sigma_1^2), \quad e_{2(ijk)} \sim N(0, \sigma_2^2)
\tag{3.1}\]
자료의 구성
이제 실험자료를 입력하여 데이터프레임으로 만들어 보자
<- as.factor (rep (c ("A1" ,"A2" , "A3" ), each= 2 , times= 3 ))<- as.factor (rep (c ("B1" , "B2" , "B3" ), each= 6 ))<- c ( 81.0 , 80.2 , 84.1 , 83.2 , 85.2 , 86.1 ,83.3 , 82.7 , 86.2 , 85.4 , 86.6 , 87.2 ,81.3 , 81.9 , 83.2 , 84.2 , 86.0 , 86.4 ) <- data.frame (temp, company, y)
temp company y
1 A1 B1 81.0
2 A1 B1 80.2
3 A2 B1 84.1
4 A2 B1 83.2
5 A3 B1 85.2
6 A3 B1 86.1
7 A1 B2 83.3
8 A1 B2 82.7
9 A2 B2 86.2
10 A2 B2 85.4
11 A3 B2 86.6
12 A3 B2 87.2
13 A1 B3 81.3
14 A1 B3 81.9
15 A2 B3 83.2
16 A2 B3 84.2
17 A3 B3 86.0
18 A3 B3 86.4
시각적 분석
일단 각 처리에 대한 관측값의 평균을 구해보자.
<- df %>% group_by (temp, company) %>% summarise (mean= mean (y), sd= sd (y))
# A tibble: 9 × 4
# Groups: temp [3]
temp company mean sd
<fct> <fct> <dbl> <dbl>
1 A1 B1 80.6 0.566
2 A1 B2 83 0.424
3 A1 B3 81.6 0.424
4 A2 B1 83.6 0.636
5 A2 B2 85.8 0.566
6 A2 B3 83.7 0.707
7 A3 B1 85.6 0.636
8 A3 B2 86.9 0.424
9 A3 B3 86.2 0.283
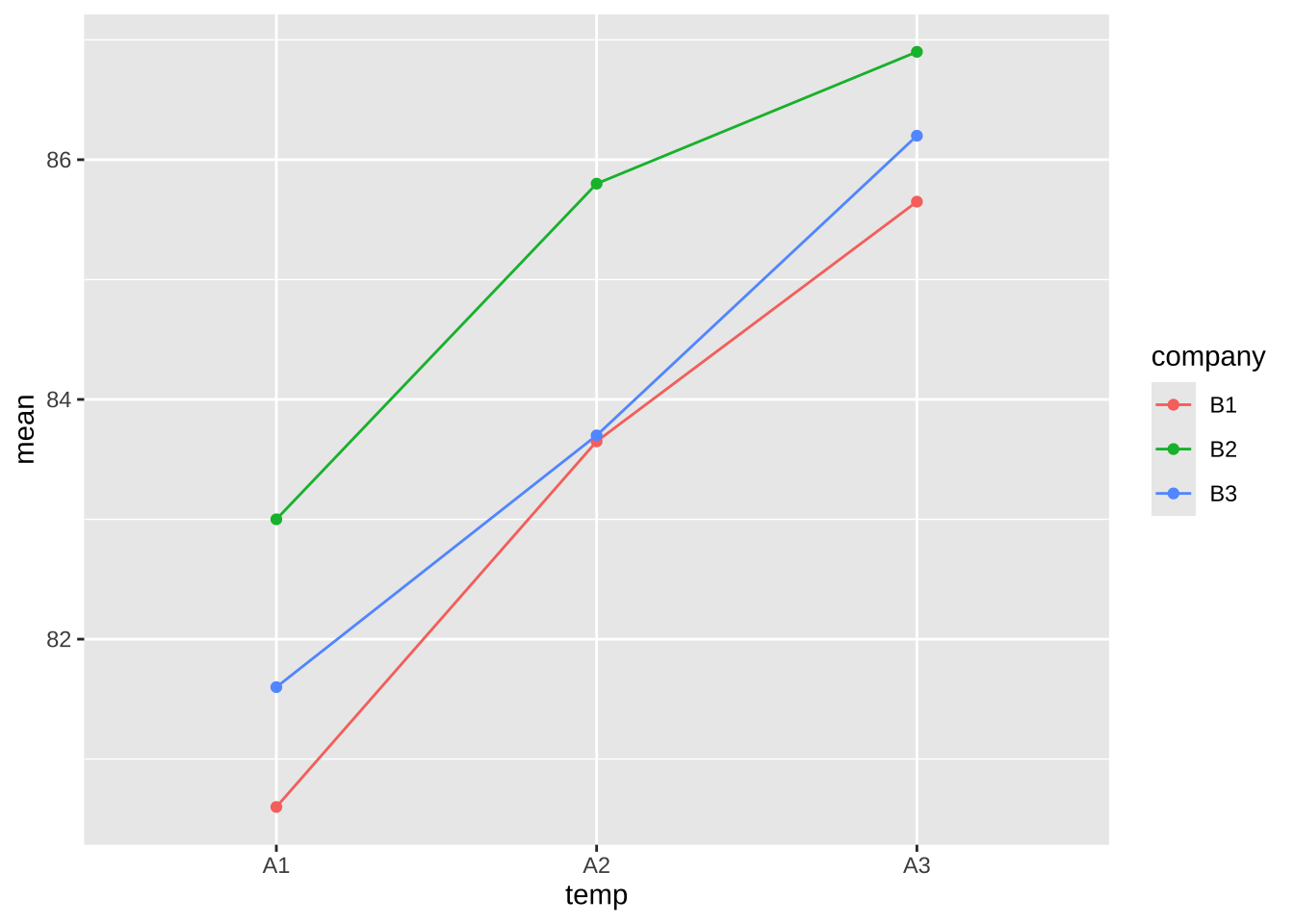
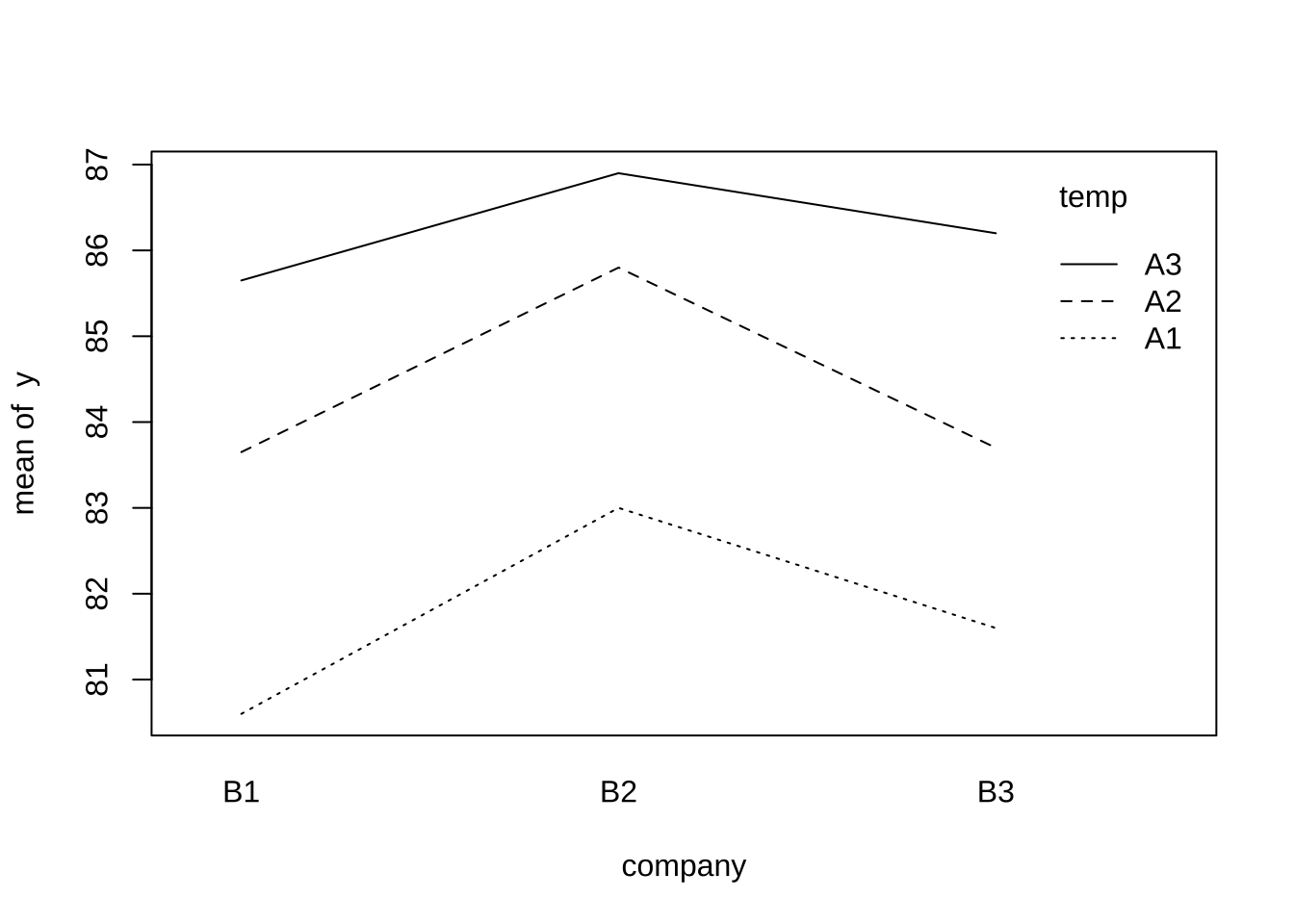
이제 처리의 평균값을 가지고 온도에 따른 변화를 살펴보자. 이 경우 제조회사 원료에 대해서는 색깔을 다르게 하여 상호작용 효과도 볼 수 있다.
아래 상호작용 그림을 보면 온도에 따라서 화학약품의 생성률이 크게 변하는 것을 알 수 있다. 유의한 상호작용은 관측되지 않는다.
%>% ggplot (aes (x = temp , y = mean, color= company)) + geom_line (aes (group = company)) + geom_point ()
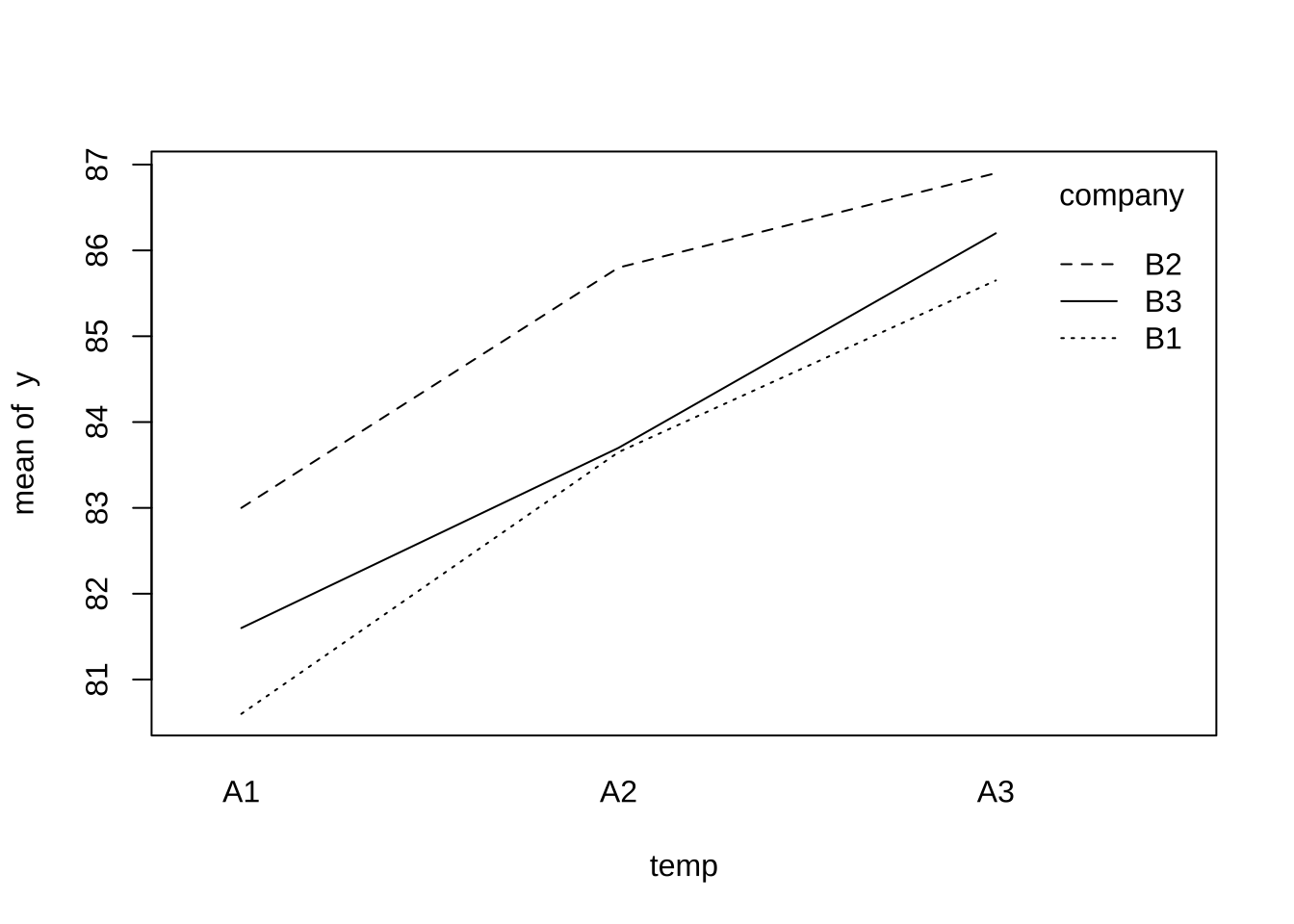
함수 interaction.plot()은상호작용 그림을 평균값을 계산하지 않고 원래 자료를 이용하여 다음과 같이 그릴 수 있다.
with (df, interaction.plot (x.factor = temp, trace.factor = company, response = y))
위에서 함수 with() 은 이용하고자 하는 변수가 있는 데이터프레임을 지정하는데사용한다. 함수 with()의 첫 번쨰 인자는 앞의 예제와 같이 df 와 같은 데이터 프레임을 지정한다. 두 번째 인자에는 함수를 이용한 명령문을 넣어준다. 앞의 프로그램에서 함수 interaction.plot() 안에서 사용된 변수들( temp,company,y)들은 데이터프레임 df에 있는 변수들이다.
이제 제조회사에 따른 변화를 살펴보자. 제조회사에 따른 생성률의 변화는 크지 않다.
with (df, interaction.plot (x.factor = company, trace.factor = temp , response = y))
분산분석
이제 분산분석을 하여 처리의 효과에 대한 검정을 해보자. 실험에서 각 처리의 조합을 블럭으로 해주어야 한다.
다음 anova 함수에서 두 처리의 조합을 temp:company 로 표시한다. 사실 temp:company는 두 처리 temp와 company의 상호작용(interaction)을 의미한다. 다음으로 처리의 조합 temp:company 이 임의효과라는 것을 Error(temp:company)와 같이 지정해 준다.
<- aov (y ~ temp + company + Error (temp: company), data= df)summary (model)
Error: temp:company
Df Sum Sq Mean Sq F value Pr(>F)
temp 2 61.81 30.907 85.72 0.00052 ***
company 2 11.96 5.982 16.59 0.01157 *
Residuals 4 1.44 0.361
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 9 2.57 0.2856
위의 분산분석표에서 온도의 효과를 검정하는 F-통계량의 값은 85.7211094 이고 p-값은 5.1981853^{-4}이다. 따라서 5% 유의수준으로 귀무가설을 기각하며 온도에 따라서 생성률이 매우 유의하게 다르다.
온도의 효과를 검정하는 F-통계량의 값은 16.5916795 이고 p-값은 0.0115724이다. 따라서 5% 유의수준으로 귀무가설을 기각하며 원료 제조회사에 따라서도 생성률이 유의하게 다르다.
블럭을 고려하지 않는 경우
만약에 처리 조합으로 생긴 블럭효과를 고려하지 않으면 어떤 일이 일어날까?
만약 생성률 실험자료를 완전 랜덤화 이원배치법 에 의하여 얻은 자료라고 생각한다면 반복이 있으므로 상호작용 효과를 추론할 수 있다. 따라서 상호작용 효과를 고정효과로 놓고 분산분석을 적용할 것이다.
\[
\rho_{ij} = (\alpha \beta)_{ij} : \text{ fixed effect }, \quad e_{2(ijk)} \sim N(0, \sigma_2^2)
\tag{3.2}\]
아래 프로그램은 상호작용 효과를 고정효과로 생각한 것이다.
<- aov (y ~ temp + company + temp: company, data= df)summary (model2)
Df Sum Sq Mean Sq F value Pr(>F)
temp 2 61.81 30.907 108.235 5.07e-07 ***
company 2 11.96 5.982 20.949 0.000411 ***
temp:company 4 1.44 0.361 1.263 0.352665
Residuals 9 2.57 0.286
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
분산분석의 결과는 위와 같으며 온도와 제조회사에 대한 F-검정 통계량을 보면 임의효과 모형에서 나온 것보다 크다. 이는 F-검정 통계량을 만들 때 분모에 사용된 평균 오차제곱합 \(MS_E\) 와 자유도가 달라서 나타나는 현상이다. 또한 자유도도
두 모형에서 온도에 대한 F-검정의 차이를 보자.
임의효과 모형 식 3.1
Error(temp:company)30.9072222
0.3605556
85.7211094
고정효과 모형 식 3.2
temp:company30.9072222
0.2855556
108.2354086
위의 표에서와 같이 실험계획에 따라서 나누어 주는 평균 오차제곱합 \(MS_E\) 와 자유도가 다르기 때문에 검정의 결과가 다르게 나타난다.
실험계획에서 통계적 추론을 하는 경우 자료의 구조는 같아도 실험의 방법(랜덤화의 방법)이 다르면 가설검정의 방법이 다르다.
따라서 실험의 방법에 따른 적절한 통계적 추론 방법을 선택하는 것이 중요하다.
혼합모형
처리들의 조합을 임의효과로 보는 모형 식 3.1 을 lmer로 적합시키는 프로그램은 다음과 같다.
분산분석 결과는 anova() 에서 임의효과 Error(temp:company)를 사용하는 결과와 동일하다.
<- lmer (y ~ temp + company + (1 | temp: company ), data = df)summary (fit)
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: y ~ temp + company + (1 | temp:company)
Data: df
REML criterion at convergence: 29.4
Scaled residuals:
Min 1Q Median 3Q Max
-1.52027 -0.46728 -0.07111 0.77604 1.20140
Random effects:
Groups Name Variance Std.Dev.
temp:company (Intercept) 0.0375 0.1936
Residual 0.2856 0.5344
Number of obs: 18, groups: temp:company, 9
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 80.9111 0.3165 4.0000 255.666 1.4e-09 ***
tempA2 2.6500 0.3467 4.0000 7.644 0.00157 **
tempA3 4.5167 0.3467 4.0000 13.028 0.00020 ***
companyB2 1.9333 0.3467 4.0000 5.577 0.00507 **
companyB3 0.5333 0.3467 4.0000 1.538 0.19877
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) tempA2 tempA3 cmpnB2
tempA2 -0.548
tempA3 -0.548 0.500
companyB2 -0.548 0.000 0.000
companyB3 -0.548 0.000 0.000 0.500
Type III Analysis of Variance Table with Satterthwaite's method
Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
temp 48.956 24.4782 2 4 85.721 0.0005198 ***
company 9.476 4.7379 2 4 16.592 0.0115724 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
분할법
전자제품 수명
다음은 교재 분할법 II - 예제 5.4 - 전자제품 수명 실험을 분석하는 예제이다.
전자부품의 수명이 온도(580, 600, 620, 640도)와 시간(5, 10, 15분)에 의해 어떤 영향을 받는지에 대한 실험이다.
이 실험은 split-plot 설계를 적용하여 관측값을 얻었다. 온도를 먼저 랜덤하게 선택하고 선택된 온도에서 3개의 가열 시간에 대한 실험을 임의 순서로 진행하였다. 또한 각 실험은 3번 반복 하였다.
온도 (temp, \(\alpha\) ) : 주구, main plot - 1차 랜덤화 요인
시간 (time, \(\beta\) ) : 분할구, split-plot, sub-plot - 2차 랜덤화 요인
반복 (rep, \(r\) ) : 반복 요인
\[
x_{ijk} = \mu + r_k + \alpha_i + \gamma_{ik} + \beta_j + (\alpha \beta)_{ij} + e_{2(ijk)}
\tag{3.3}\]
위의 모형식에서 반복과 온도의 상호작용 효과 \(( \alpha r)_{ik}\) 와 1차 랜덤화에 의한 오차 \(e_{1(ik)}\) 는 교락되어 블럭효과 \(\gamma_{ik}\) 에 합쳐저서 나타난다.
\[ \gamma_{ik} = (\alpha r)_{ik} + e_{1(ik)} \]
자료의 구성
이제 실험자료를 입력하여 데이터프레임으로 만들어 보자
<- as.factor (rep (c (1 : 3 ), each= 12 ))<- as.factor (rep (c (580 , 600 , 620 , 640 ), each= 3 , times= 3 ))<- as.factor (rep (c (5 , 10 , 15 ), times= 12 ))<- c (217 , 233 , 175 , 158 , 138 , 152 , 229 , 186 , 155 , 223 , 227 , 156 ,188 , 201 , 195 , 126 , 130 , 147 , 160 , 170 , 161 , 201 , 181 , 172 ,162 , 170 , 213 , 122 , 185 , 180 , 167 , 181 , 182 , 182 , 201 , 199 ) <- data.frame (rep, temp, time, y)
함수 xtab 을 이용하면 반복에 따라서 자료 구조를 쉽게 볼 수 있다.
xtabs ( y ~ time + temp + rep, df)
, , rep = 1
temp
time 580 600 620 640
5 217 158 229 223
10 233 138 186 227
15 175 152 155 156
, , rep = 2
temp
time 580 600 620 640
5 188 126 160 201
10 201 130 170 181
15 195 147 161 172
, , rep = 3
temp
time 580 600 620 640
5 162 122 167 182
10 170 185 181 201
15 213 180 182 199
시각적 분석
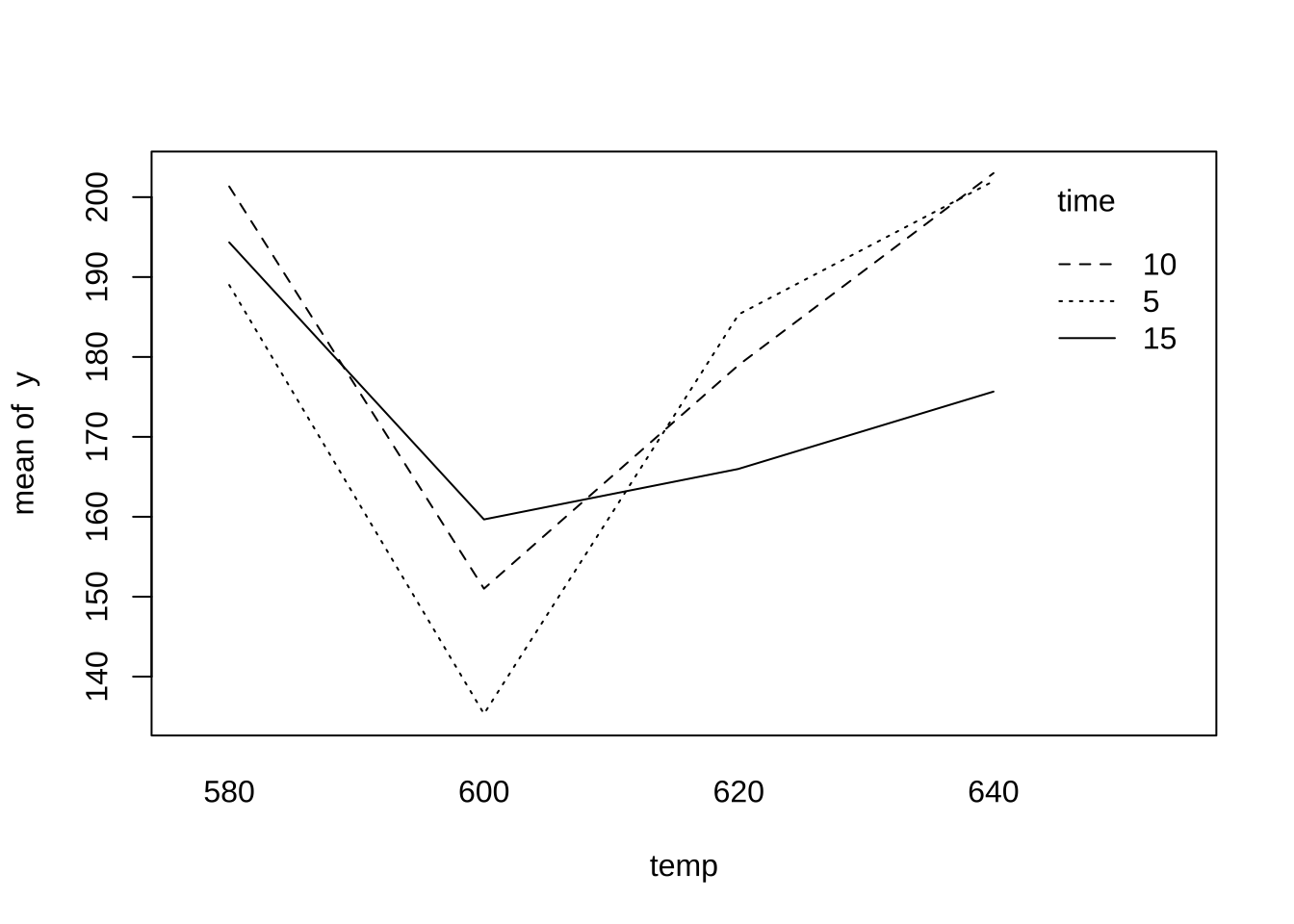
이제 온도의 수준에 따른 변화를 볼 수 있는 그림을 그려보자. 온도가 증가하면서 수명이 줄어들었다가 다시 늘어나는 현상을 볼 수 있다.
with (df, interaction.plot (x.factor = temp, trace.factor = time, response = y))
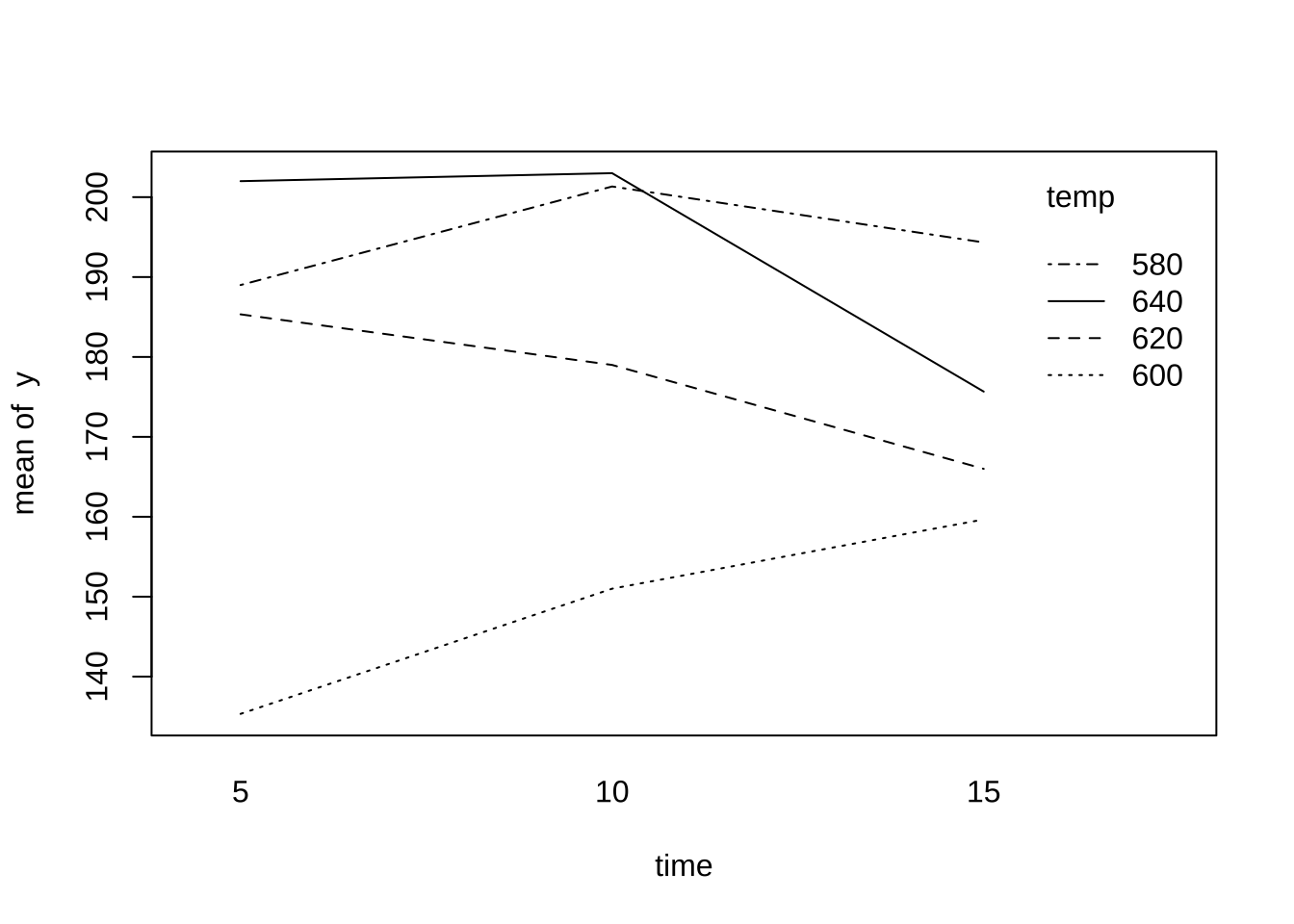
가열시간의 수준에 따른 변화를 볼 수 있는 그림을 그려보자. 가열시간이 증가하더러도 수명이 크게 변하지 않는 것을 알 수 있다.
with (df, interaction.plot (x.factor = time, trace.factor = temp, response = y))
분산분석
이제 모형식 식 3.3 에 대한 분산분석을 실시해 보자.
여기서 유의할 점은 모형식 식 3.3 에서 블럭효과 \(\gamma_{ik}\) 는 임의효과로 생각하며 반복 수준과 온도 수준의 조합이다. 따라서 블럭효과 \(\gamma_{ik}\) 에 대한 항을 Error(rep:temp)로 사용한다.
\[ \gamma_{ik} \sim N(0,\sigma^2_1), \quad e_{2(ijk)} \sim N(0, \sigma^2_E) \]
<- aov (y ~ rep + temp* time + Error (rep: temp), data= df)summary (model)
Error: rep:temp
Df Sum Sq Mean Sq F value Pr(>F)
rep 2 1963 981 3.319 0.107
temp 3 12494 4165 14.086 0.004 **
Residuals 6 1774 296
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
time 2 566 283.1 0.456 0.642
temp:time 6 2600 433.4 0.698 0.655
Residuals 16 9933 620.8
분산분석표에서 온도의 효과를 검정하는 F-통계량의 값은 14.0864677 이고 p-값은 0.0040028이다. 따라서 5% 유의수준으로 귀무가설을 기각하며 온도에 따라서 제품의 수명이 유의하게 다르다.
가열시간의 효과를 검정하는 F-통계량의 값은 0.4560179 이고 p-값은 0.6417897이다. 따라서 5% 유의수준으로 귀무가설을 기각할 수 없으며 가열시간에 따라서 제품의 수명이 다르지 않다.
온도와 가열시간의 상호작용 효과를 검정하는 F-통계량의 값은 0.6981059 이고 p-값은 0.655133이다. 따라서 5% 유의수준으로 귀무가설을 기각할 수 없으며 상호작용은 유의하지 않다.