일원배치: 예제와 R 프로그램
예제: 실험계획
4개의 서로 다른 원단업체에서 직물을 공급받고 있다. 공급한 직물의 긁힘에 대한 저항력을 알아보기 위하여 각 업체마다 4개의 제품을 랜덤하게 선택하여 (\(a=4\) , \(r=4\) ) 일원배치법에 의하여 마모도 검사을 실시하였다.
자료의 생성
<- as.factor (rep (c (1 : 4 ), each= 4 ))<- c (1.93 , 2.38 , 2.20 , 2.25 ,2.55 , 2.72 , 2.75 , 2.70 ,2.40 , 2.68 , 2.32 , 2.28 ,2.33 , 2.38 , 2.28 , 2.25 )<- data.frame (company= company, response= response)
company response
1 1 1.93
2 1 2.38
3 1 2.20
4 1 2.25
5 2 2.55
6 2 2.72
7 2 2.75
8 2 2.70
9 3 2.40
10 3 2.68
11 3 2.32
12 3 2.28
13 4 2.33
14 4 2.38
15 4 2.28
16 4 2.25
각 수준에 대한 표본 평균을 구해보자.
<- df31 %>% group_by (company) %>% summarise (mean= mean (response), median= median (response), sd= sd (response), min= min (response), max= max (response))
# A tibble: 4 × 6
company mean median sd min max
<fct> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 2.19 2.22 0.189 1.93 2.38
2 2 2.68 2.71 0.0891 2.55 2.75
3 3 2.42 2.36 0.180 2.28 2.68
4 4 2.31 2.30 0.0572 2.25 2.38
선형모형의 적합(set-to-zero)
이제 자료를 다음과 같은 선형 모형으로 적합해 보자. 선형 모형의 적합은 lm() 함수를 사용한다.
\[ y_{ij} = \mu + \alpha_i + e_{ij} \]
여기서 선형식의 모수와 R의 변수는 다음과 같은 관계를 가진다,
\(\mu\) (Intercept)
\(\alpha_1\) company1
\(\alpha_2\) company2
\(\alpha_3\) company3
\(\alpha_4\) company4
<- lm (response~ company,data= df31)summary (fit1)
Call:
lm(formula = response ~ company, data = df31)
Residuals:
Min 1Q Median 3Q Max
-0.2600 -0.0700 0.0150 0.0625 0.2600
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.19000 0.07050 31.062 7.79e-13 ***
company2 0.49000 0.09971 4.914 0.000357 ***
company3 0.23000 0.09971 2.307 0.039710 *
company4 0.12000 0.09971 1.204 0.251982
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.141 on 12 degrees of freedom
Multiple R-squared: 0.6871, Adjusted R-squared: 0.6089
F-statistic: 8.785 on 3 and 12 DF, p-value: 0.002353
위에서 적합한 결과를 보면 평균 \(\mu\) 와 4개의 처리 \(\alpha_1\) , \(\alpha_2\) , \(\alpha_3\) , \(\alpha_4\) 가 모형에 있지만 모수의 추정량은 평균(intercept)과 3개의 모수(company2, company3, company4)만 추정량이 주어진다.
R 에서 옵션을 지정하지 않고 함수 lm()으로 선형모형을 적합하는 경우 set-to-zero 조건을 적용하며 자료에 나타난 처리의 수준들 중 순위가 가장 낮은 수준의 효과를 0으로 지정한다 (company1=0 ). set-to-zero 조건을 강제로 지정하려면 다음과 같은 명령문을 먼저 실행한다.
options(contrasts=c("contr.treatment", "contr.poly"))위의 결과를 보면 (Intercept)에 대한 추정량이 첫 번째 처리 company1의 평균과 같은 것을 알 수 있다.
set-to-zero 조건에서의 계획행렬은 다음과 같이 볼 수 있다.
(Intercept) company2 company3 company4
1 1 0 0 0
2 1 0 0 0
3 1 0 0 0
4 1 0 0 0
5 1 1 0 0
6 1 1 0 0
7 1 1 0 0
8 1 1 0 0
9 1 0 1 0
10 1 0 1 0
11 1 0 1 0
12 1 0 1 0
13 1 0 0 1
14 1 0 0 1
15 1 0 0 1
16 1 0 0 1
attr(,"assign")
[1] 0 1 1 1
attr(,"contrasts")
attr(,"contrasts")$company
[1] "contr.treatment"
이제 각 처리 평균에 대한 추정값 \(\widehat{\mu+ \alpha_i}\) 을 구해보자.
company emmean SE df lower.CL upper.CL
1 2.19 0.0705 12 2.04 2.34
2 2.68 0.0705 12 2.53 2.83
3 2.42 0.0705 12 2.27 2.57
4 2.31 0.0705 12 2.16 2.46
Confidence level used: 0.95
이 경우 처리 평균에 대한 추정값은 산술 평균과 동일하게 나온다.
선형모형의 적합 (sum-to-zero)
이제 일원배치 모형에서 sum-to-zero 조건을 적용하여 모수를 추정해 보자. sum-to-zero 조건을 적용하려면 다음과 같은 명령어를 실행해야 한다.
options (contrasts= c ("contr.sum" , "contr.poly" ))
이제 다시 선형모형을 적합하고 추정결과를 보자.
<- lm (response~ company,data= df31)summary (fit2)
Call:
lm(formula = response ~ company, data = df31)
Residuals:
Min 1Q Median 3Q Max
-0.2600 -0.0700 0.0150 0.0625 0.2600
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.40000 0.03525 68.081 < 2e-16 ***
company1 -0.21000 0.06106 -3.439 0.004901 **
company2 0.28000 0.06106 4.586 0.000626 ***
company3 0.02000 0.06106 0.328 0.748892
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.141 on 12 degrees of freedom
Multiple R-squared: 0.6871, Adjusted R-squared: 0.6089
F-statistic: 8.785 on 3 and 12 DF, p-value: 0.002353
이제 sum-to-zero 조건에 따라서 위의 set-to-zero 결과와 모수의 추정값이 다르게 나타나는 것을 알 수 있다. 마지막 모수 company4(\(\alpha_4\) )는 sum-to-zero 조건을 이용하여 다음과 같은 관계를 이용하여 구할 수 있다.
\[ \alpha_4 = -(\alpha_1 + \alpha_2 + \alpha_3) \]
sum-to-zero 조건에서의 계획행렬은 다음과 같이 볼 수 있다.
(Intercept) company1 company2 company3
1 1 1 0 0
2 1 1 0 0
3 1 1 0 0
4 1 1 0 0
5 1 0 1 0
6 1 0 1 0
7 1 0 1 0
8 1 0 1 0
9 1 0 0 1
10 1 0 0 1
11 1 0 0 1
12 1 0 0 1
13 1 -1 -1 -1
14 1 -1 -1 -1
15 1 -1 -1 -1
16 1 -1 -1 -1
attr(,"assign")
[1] 0 1 1 1
attr(,"contrasts")
attr(,"contrasts")$company
[1] "contr.sum"
이제 각 처리 평균에 대한 추정값 \(\widehat{\mu+ \alpha_i}\) 을 구해보면 set-to-zero 조건에서의 추정값과 동일함을 알 수 있다.
company emmean SE df lower.CL upper.CL
1 2.19 0.0705 12 2.04 2.34
2 2.68 0.0705 12 2.53 2.83
3 2.42 0.0705 12 2.27 2.57
4 2.31 0.0705 12 2.16 2.46
Confidence level used: 0.95
분산분석
분산분석의 결과는 어떠한 제약 조건에서도 동일하다.
Analysis of Variance Table
Response: response
Df Sum Sq Mean Sq F value Pr(>F)
company 3 0.5240 0.174667 8.7846 0.002353 **
Residuals 12 0.2386 0.019883
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Analysis of Variance Table
Response: response
Df Sum Sq Mean Sq F value Pr(>F)
company 3 0.5240 0.174667 8.7846 0.002353 **
Residuals 12 0.2386 0.019883
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
다중비교 예제
앞에서 살펴본 일원배치법 예제은 4개의 처리가 있다. 따라서 \({4 \choose 2} =6\) 개의 가설 검정(또는 신뢰구간)을 수행해야 한다.
4개의 company가 처리 수준이며 각 처리수준 은 1, 2, 3, 4로 표시된다.
# A tibble: 4 × 6
company mean median sd min max
<fct> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 2.19 2.22 0.189 1.93 2.38
2 2 2.68 2.71 0.0891 2.55 2.75
3 3 2.42 2.36 0.180 2.28 2.68
4 4 2.31 2.30 0.0572 2.25 2.38
다중비교 방법을 적용하지 않는 경우
먼저 다중비교 방법을 적용하지 않는 경우 결과를 보자. 함수 LSD.test 에서 p.adj=c("none")를 지정하면 다중 비교를 적용하지 않는다. 명령문 p.adj 를 지정하지 않으면 수정을 하지 않는 LSD 방법에 의한 신뢰 구간 식 7.24 와 검정 방법 식 7.25 로 구한 결과를 준다.
<- aov (response~ company,data= df31) #일원배치 <- LSD.test (anova.res, "company" , alpha = 0.05 , group = FALSE , console = FALSE , p.adj= c ("none" ) )$ comparison
difference pvalue signif. LCL UCL
1 - 2 -0.49 0.0004 *** -0.70724487 -0.27275513
1 - 3 -0.23 0.0397 * -0.44724487 -0.01275513
1 - 4 -0.12 0.2520 -0.33724487 0.09724487
2 - 3 0.26 0.0229 * 0.04275513 0.47724487
2 - 4 0.37 0.0030 ** 0.15275513 0.58724487
3 - 4 0.11 0.2916 -0.10724487 0.32724487
본페로니 수정(Bonferroni correction)
이제 다중비교 방법 중에 가장 보수적인 본페로니 수정(Bonferroni correction)을 적용해 보자. 함수 LSD.test 에서 p.adj=c("bonferroni")를 이용한다.
아래의 결과는 본페로니 수정 방법에 의한 신뢰 구간 와 검정 방법으로 구한 결과이다.
본페로니 수정이 적용된 신뢰구간은 LSD 방법의 신뢰구간보다 길며 수정된 p-값은 LSD 방법으로 구한 값의 6배이다. LSD 방법을 적용하는 경우 유의한 차이를 보이는 조합이 4개로 나타났는데(1-2,1-3,2-3,2-4) 본페로니 수정을 적용한 경우에는 2개로 줄어 들었다(1-2,2-4)
수정한 p-값이 1이 초과하면 확률이기 때문에 1로 주어진다.
<- LSD.test (anova.res, "company" , alpha = 0.05 , group = FALSE , console = FALSE , p.adj= c ("bonferroni" ) )$ comparison
difference pvalue signif. LCL UCL
1 - 2 -0.49 0.0021 ** -0.80434725 -0.17565275
1 - 3 -0.23 0.2383 -0.54434725 0.08434725
1 - 4 -0.12 1.0000 -0.43434725 0.19434725
2 - 3 0.26 0.1374 -0.05434725 0.57434725
2 - 4 0.37 0.0179 * 0.05565275 0.68434725
3 - 4 0.11 1.0000 -0.20434725 0.42434725
Tukey의 HSD
함수TukeyHSD는 분산분석을 실행한 결과를 이용하여 다중비교 방법 중 가장 많이 이용되는 Tukey’s Honest Significant Difference (HSD) 방법으로 다중비교를 제공한다.
Tukey의 HSD는 너무 보수적인 결과를 주는 본페로니 수정을 개선한 것이다. 따라서 Tukey의 HSD 에서 얻은 결과는 수정하지 않는 LDS 의 결과와 Bonferoni 방법의 중간에 있다고 할 수 있다.
Tukey의 HSD 에서는 본페로니와 유사하게 2개의 조합(1-2,2-4)만이 유의한 차이가 있다고 나타난다.
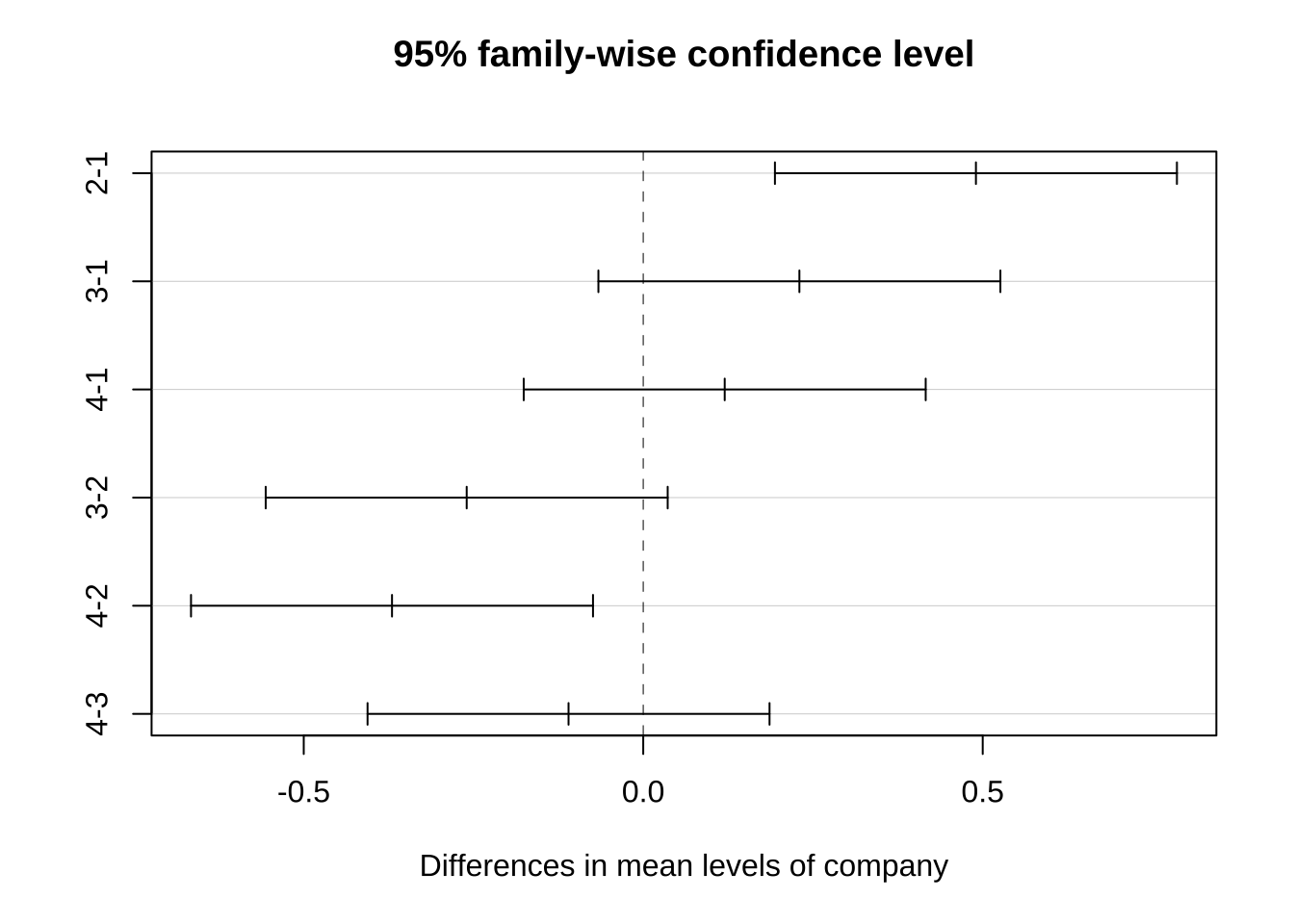
<- aov (response~ company,data= df31) #일원배치 <- TukeyHSD (anova.res, conf.level = 0.95 , ordered= FALSE )
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = response ~ company, data = df31)
$company
diff lwr upr p adj
2-1 0.49 0.19397708 0.78602292 0.0017496
3-1 0.23 -0.06602292 0.52602292 0.1509207
4-1 0.12 -0.17602292 0.41602292 0.6362891
3-2 -0.26 -0.55602292 0.03602292 0.0924227
4-2 -0.37 -0.66602292 -0.07397708 0.0136804
4-3 -0.11 -0.40602292 0.18602292 0.6943908
세 방법에서의 p-값 비교
위에서 살펴본 수정을 하지 않은 LSD 방법, Tukey의 HSD 방법과 본페로니 방법에서 계산된 p-값을 아래 표에서 비교하였다.
LSD, Bonferoni, HSD 방법의 p-값 비교
1-2
0.0004
0.0017
0.0021
1-3
0.0397
0.1509
0.2383
1-4
0.2520
0.6363
1.0000
2-3
0.0229
0.0924
0.1374
2-4
0.0030
0.0137
0.0179
3-4
0.2916
0.6944
1.0000
예제 7.1 - 일원배치
이제 교재 예제 7.1 (271 페이지)에서 관고비 자료 adsale에서 판매액을 예측하는 회귀식을 고려해 보자.
먼저 adsale 데이터프레임에서 두 변수 광고비 ad 와 매체 media 변수의 차이점을 알아보자. 먼저 광고비 ad는 수치 변수(numeric variable)로서 함수 class()를 이용하면 정수(integer) 형태인 것을 알 수 있다. 수치변수는 정수, 실수, 복소수 등을 의미한다.
반면 매체 media 는 범주형 변수로서 함수 class()를 이용하면 범주형(factor) 형태인 것을 알 수 있다. levels는 범주형 변수의 항목을 나타내는 것으로서 범주형 변수 media는 두 개의 항목 방송과 신문으로 이루어 졌음을 알 수 있다.
sale ad media
1 39 4 방송
2 42 6 신문
3 45 6 방송
4 47 8 신문
5 50 8 방송
6 50 9 신문
[1] 4 6 6 8 8 9 9 10 12 12
[1] 방송 신문 방송 신문 방송 신문 방송 방송 신문 방송
Levels: 방송 신문
그룹별 기초통계량을 계산해보자.
<- adsale %>% group_by (media) %>% summarise (mean= mean (ad), median= median (ad), sd= sd (ad), min= min (ad), max= max (ad))
# A tibble: 2 × 6
media mean median sd min max
<fct> <dbl> <dbl> <dbl> <int> <int>
1 방송 8.17 8.5 2.86 4 12
2 신문 8.75 8.5 2.5 6 12
함수 lm()으로 선형모형을 적합하는 경우 set-to-zero 조건을 적용하며 자료에 나타난 처리의 수준들 중 순위가 가장 낮은 수준의 효과를 0으로 지정한다 set-to-zero 조건을 강제로 지정하려면 다음과 같은 명령문을 먼저 실행한다.
options (contrasts= c ("contr.treatment" , "contr.poly" ))
이제 광고비 ad 와 매체 media 를 포함한 회귀식을 적합시켜 보자. R의 lm 함수는 범주형변수를 자동적으로 가변수로 바꾸어 준다. 회귀식에 사용된 디자인행렬을 보면 media에 해당하는 열이 0 과 1로 이루어진 벡터로 바뀌었음을 알 수 있다.
<- lm (sale~ ad + media, data= adsale)summary (fit1)
Call:
lm(formula = sale ~ ad + media, data = adsale)
Residuals:
Min 1Q Median 3Q Max
-0.47902 -0.24720 0.02727 0.22832 0.39091
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.21888 0.38588 75.72 1.84e-11 ***
ad 2.56503 0.04408 58.19 1.16e-10 ***
media신문 -2.66294 0.22114 -12.04 6.21e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3403 on 7 degrees of freedom
Multiple R-squared: 0.998, Adjusted R-squared: 0.9974
F-statistic: 1707 on 2 and 7 DF, p-value: 3.875e-10
(Intercept) ad media신문
1 1 4 0
2 1 6 1
3 1 6 0
4 1 8 1
5 1 8 0
6 1 9 1
7 1 9 0
8 1 10 0
9 1 12 1
10 1 12 0
attr(,"assign")
[1] 0 1 2
attr(,"contrasts")
attr(,"contrasts")$media
[1] "contr.treatment"
data.frame (media= adsale$ media, z= model.matrix (fit1)[,3 ])
media z
1 방송 0
2 신문 1
3 방송 0
4 신문 1
5 방송 0
6 신문 1
7 방송 0
8 방송 0
9 신문 1
10 방송 0
예제 7.2 - 교호작용
<- lm (sale ~ ad + media + ad: media, data= adsale)summary (fit2)
Call:
lm(formula = sale ~ ad + media + ad:media, data = adsale)
Residuals:
Min 1Q Median 3Q Max
-0.3674 -0.1400 -0.1043 0.2194 0.4490
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 29.00000 0.46388 62.516 1.13e-09 ***
ad 2.59184 0.05411 47.901 5.55e-09 ***
media신문 -1.93333 0.85628 -2.258 0.0647 .
ad:media신문 -0.08517 0.09645 -0.883 0.4112
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3458 on 6 degrees of freedom
Multiple R-squared: 0.9982, Adjusted R-squared: 0.9973
F-statistic: 1102 on 3 and 6 DF, p-value: 1.298e-08
Analysis of Variance Table
Response: sale
Df Sum Sq Mean Sq F value Pr(>F)
ad 1 378.50 378.50 3166.1379 2.116e-09 ***
media 1 16.79 16.79 140.4378 2.183e-05 ***
ad:media 1 0.09 0.09 0.7797 0.4112
Residuals 6 0.72 0.12
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Intercept) ad media신문 ad:media신문
1 1 4 0 0
2 1 6 1 6
3 1 6 0 0
4 1 8 1 8
5 1 8 0 0
6 1 9 1 9
7 1 9 0 0
8 1 10 0 0
9 1 12 1 12
10 1 12 0 0
attr(,"assign")
[1] 0 1 2 3
attr(,"contrasts")
attr(,"contrasts")$media
[1] "contr.treatment"
예제 7.3 - 일원배치 2
score grade
1 81 1
2 75 1
3 69 1
4 90 1
5 72 1
6 83 1
7 65 2
8 80 2
9 73 2
10 79 2
11 81 2
12 69 2
13 72 3
14 67 3
15 62 3
16 76 3
17 80 3
18 89 4
19 94 4
20 79 4
21 88 4
위의 결과로 보면 변수 grade는 수치형 변수이다. 따라서 이를 범주형 변수로 바꾸어 주어야 한다. 위의 명령문은 함수 factor()를 사용하여 수치 변수인 grade를 항목의 순서가 4,1,2,3 (levels=c(4,1:3)) 인 범주형 변수로 바꾸어 주는 것이다.
$ grade <- factor (english1$ grade, levels= c (4 , 1 : 3 ), labels = c ("4학년" , "1학년" , "2학년" , "3학년" ))$ grade
[1] 1학년 1학년 1학년 1학년 1학년 1학년 2학년 2학년 2학년 2학년 2학년 2학년
[13] 3학년 3학년 3학년 3학년 3학년 4학년 4학년 4학년 4학년
Levels: 4학년 1학년 2학년 3학년
그룹별 기초통계량을 계산해보자.
<- english1 %>% group_by (grade) %>% summarise (mean= mean (score), median= median (score), sd= sd (score), min= min (score), max= max (score))
# A tibble: 4 × 6
grade mean median sd min max
<fct> <dbl> <dbl> <dbl> <int> <int>
1 4학년 87.5 88.5 6.24 79 94
2 1학년 78.3 78 7.79 69 90
3 2학년 74.5 76 6.57 65 81
4 3학년 71.4 72 7.13 62 80
이제 일원배치모형을 적합시키고 ANOVA F-검정을 수행해 보자.
<- lm (score ~ grade, english1)summary (fit3)
Call:
lm(formula = score ~ grade, data = english1)
Residuals:
Min 1Q Median 3Q Max
-9.500 -5.500 0.600 4.667 11.667
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 87.500 3.513 24.910 8.06e-15 ***
grade1학년 -9.167 4.535 -2.021 0.05927 .
grade2학년 -13.000 4.535 -2.867 0.01069 *
grade3학년 -16.100 4.713 -3.416 0.00329 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.025 on 17 degrees of freedom
Multiple R-squared: 0.4341, Adjusted R-squared: 0.3342
F-statistic: 4.347 on 3 and 17 DF, p-value: 0.01905
Analysis of Variance Table
Response: score
Df Sum Sq Mean Sq F value Pr(>F)
grade 3 643.63 214.544 4.347 0.01905 *
Residuals 17 839.03 49.355
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
적합한 모형을 이용하여 최소제곱 평균을 구해보자.
grade emmean SE df lower.CL upper.CL
4학년 87.5 3.51 17 80.1 94.9
1학년 78.3 2.87 17 72.3 84.4
2학년 74.5 2.87 17 68.4 80.6
3학년 71.4 3.14 17 64.8 78.0
Confidence level used: 0.95
다중비교 방법을 적용하지 않고 각 학년별 평균의 차이를 비교하자.
<- aov (fit3)<- LSD.test (anova.res, "grade" , alpha = 0.05 , group = FALSE , console = FALSE , p.adj= c ("none" ) )$ comparison
difference pvalue signif. LCL UCL
1학년 - 2학년 3.833333 0.3579 -4.724208 12.3908748
1학년 - 3학년 6.933333 0.1215 -2.041892 15.9085586
1학년 - 4학년 -9.166667 0.0593 . -18.734289 0.4009556
2학년 - 3학년 3.100000 0.4761 -5.875225 12.0752252
2학년 - 4학년 -13.000000 0.0107 * -22.567622 -3.4323777
3학년 - 4학년 -16.100000 0.0033 ** -26.042965 -6.1570353
본페로니 수정(Bonferroni correction)을 적용하여 각 학년별 평균의 차이를 비교하자.
<- LSD.test (anova.res, "grade" , alpha = 0.05 , group = FALSE , console = FALSE , p.adj= c ("bonferroni" ) )$ comparison
difference pvalue signif. LCL UCL
1학년 - 2학년 3.833333 1.0000 -8.270123 15.9367895
1학년 - 3학년 6.933333 0.7292 -5.760879 19.6275452
1학년 - 4학년 -9.166667 0.3556 -22.698742 4.3654087
2학년 - 3학년 3.100000 1.0000 -9.594212 15.7942119
2학년 - 4학년 -13.000000 0.0641 . -26.532075 0.5320754
3학년 - 4학년 -16.100000 0.0197 * -30.162945 -2.0370548
다중비교 방법 중 가장 많이 이용되는 Tukey’s Honest Significant Difference (HSD) 방법으로 각 학년별 평균의 차이를 비교하자.
<- TukeyHSD (anova.res, conf.level = 0.95 , ordered= FALSE )
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = fit3)
$grade
diff lwr upr p adj
1학년-4학년 -9.166667 -22.05714 3.7238087 0.2190188
2학년-4학년 -13.000000 -25.89048 -0.1095246 0.0476922
3학년-4학년 -16.100000 -29.49617 -2.7038250 0.0157259
2학년-1학년 -3.833333 -15.36293 7.6962583 0.7813729
3학년-1학년 -6.933333 -19.02567 5.1590044 0.3891708
3학년-2학년 -3.100000 -15.19234 8.9923378 0.8842429